1. What is black body radiation?
A perfect black body is that which can absorb radiations of all the wavelengths which fall on it. It neither reflects nor refracts and so it appears black. The radiation emitted by a black body is known black body radiation.
2. What is meant by a perfect black body?
A perfect black body is the one which absorbs all the radiations that fall on it and emits radiation of all wavelengths.
3. Define Rayleigh – Jeans law. Give its limitations.
Rayleigh – Jeans state that the energy distribution is directly proportional to the absolute temperature and is inversely proportional to the fourth power of the wavelength.
i.e., \mathrm{E}_\lambda \alpha \frac{\mathrm{T}}{\lambda^4} (or) \mathrm{E}_\lambda=\frac{8 \pi \mathrm{kT}}{\lambda^4}
Limitation: It holds good only for longer wavelength.
4. Define Wien’s displacement law. Give its limitation.
It is defined as ‘the product of the wavelength (λm ) corresponding to maximum energy and the absolute temperature (T) is a constant.
i.e., λm T = constant
Limitation : It holds good only for shorter wavelengths.
5. What are the postulates of Planck’s quantum theory or Explain Planck’s hypothesis.
The postulates of Planck’s quantum theory are,
a. There are simple harmonic oscillators in the blackbody.
b. They oscillate in all possible frequencies.
c. They oscillators will not emit energy continuously.
d. They emit radiation in terms of quantas of magnitude ‘hν ’.
i.e., E = n hν,Where n = 1,2,3,4.
6. What is meant by matter wave or state de-broglie’s hypothesis?
We know nature loves symmetry, since the light exhibits the dual nature (i.e.,) it can behave both the wave. De-Broglie suggested that an electron, which is a particle can also behave as a wave and exhibits the dual nature. Thus the waves associated with a material particle (electron) are called as matter waves.
If ‘v ’ is the velocity and ‘m ’ is the mass of the particle then de-Broglie wavelength, \lambda=\frac{\mathrm{h}}{\mathrm{mv}}
7. What is meant by Photon? Given any two properties.
Definition :
Photons are discrete energy values in the form of small quantas of definite frequency (or) wavelength.
Properties :
They does not have any charge and they will not ionize.
The energy and momentum of the photon is given by
E = hν and P = mv
where, m – Mass of photon,
v – Velocity of photon,
h – Planck’s constant
n – Frequency
8. Write down Planck’s radiation formula.
Energy emitted per second per unit area per unit wavelength interval at wavelength λ,
\mathrm{E}_\lambda=\frac{8 \pi \mathrm{hc}}{\lambda^5} \times \frac{1}{\mathrm{e}^{\frac{\mathrm{h} \nu}{\mathrm{kT}}}-1}where, h – Planck’s constant,
C – Velocity of light.
λ – Wavelength of radiation,
v – Frequency of radiation,
K – Boltzmann’s constant,
T – Temperature of the body
9. What is Compton effect?
When a beam of monochromatic X-rays pass through matter, the scattered beam consists of a radiation of the same wavelength as that of the incident beam and in addition, also contains a modified radiation of slightly longer wavelength. This is called Compton effect.
10. What is Compton waverlength?
When a beam of monochromatic X-rays pass through matter, the scattered beam consists of a radiation of the same wavelength as that of the incident beam and in addition, also contains a modified radiation of slightly longer wavelength. This is called Compton effect. The change in wavelength in Compton effect is called Compton wavelength dλ.
\mathrm{d} \lambda=\lambda^{\prime}-\lambda=\frac{2 \mathrm{~h}}{\mathrm{~m}_0 \mathrm{c}} \cdot \sin ^2 \frac{\theta}{2}where, ‘ θ ’ is the photon scattered angle.
11. What is Schroedinger wave equation?
The equation that describes the wave nature of a particle in mathematical form is known as schroedinger wave equation. It is classified as
- Time independent of wave equation.
- Time dependent wave equation.
12. What to you understand by the term wave function.
Wave function ψ is a variable quantity that is associated with a moving particle at any position (x, y, z) and at any time ‘t’. it relates the probability of finding the particle at that point and at that time.
Since ψ is a complex quantity, it has no meaning and hence the probability function \psi^2=\psi \boxtimes \psi is found, which is real and positive and has physical meaning, which is a measurable quantity.
13. What is the physical significance of a wave function?
The probability of finding a particle in space, at any given instant of time is characterized by a function ψ (x,y,z) called wave function.
- It relates the particle and the wave statistically.
- It gives the information about the particle behaviour.
- It is a complex quantity.
ψ2 represents the probability density of the particle, which is real and positive.
14. Write down the schroedinger wave equation and give any two applications of it.
There are two types of schroedinger wave equations, viz.
i. Schroedinger time dependent wave equation, given by
Eψ = Hψ
Where, E – total energy of the particle,
H – Hamiltonian operator,
ψ – Wave function
ii. Schroedinger time independent wave equation, given by
\nabla^2 \psi+\frac{2 \mathrm{~m}}{\hbar^2}(\mathrm{E}-\mathrm{V}) \psi=0(3-\text { dim ensional })Where, E – total energy of the particle,
V – Potential energy of the particle
M – mass of the particle
M- h/2π (h-Planck’s constant)
Applications
- It is used to find the electrons in the metal
- It is used to find the energy levels of an electron in an infinite deep potential well.
15. Define normalization process and write down the normalized wave function for an electron in a one dimensional potential well of length ‘a’ metres.
Normalisation is the process by which the probability of finding a particle inside any potential well can be done.
For a one dimensional potential well of length ’ a ’ metre the normalized wave function is given by
\psi_{\mathrm{n}}=\sqrt{\frac{2}{\mathrm{a}}} \sin \frac{\mathrm{n} \pi \mathrm{x}}{\mathrm{a}}16. Define Eigen value and Eigen function.
Eigen value is defined as energy of the particle and is denoted by the letter
(En)Eigen function is defined as the wave function of the particle and is denoted by the letter (ψn ) .
17. What is meant by degenerate and non-degenerate state? Give examples.
Degenerate state: For various combination of quantum numbers if we get same eigen value (energy levels) but different eigen functions, then it is called degenerate state.
Example: For three combination of quantum numbers say (112), (121) and (211), we get same energy values i.e., E112 = E121 = E211 but different eigen functions i.e., ψ112≠ψ121 ψ≠211
Non-Degenerate state
For various combination of quantum numbers if we get same eigen value (energy levels) but same eigen functions, then it is called Non-degenerate state.
Example : For three combination of quantum numbers say (222) we get same energy value E222 and same eigen function ψ222.
18. Define magnifying power.
The magnifying power (M) of a microscope is defined as the ratio between the angle subtended by the final image (β) at the eye to the angle subtended by the object (α) at the eye kept at the near point.
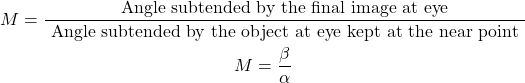
\begin{gathered} M=\frac{\text { Angle subtended by the final image at eye }}{\text { Angle subtended by the object at eye kept at the near point }} \\ M=\frac{\beta}{\alpha} \end{gathered}19. Define resolving power of microscope.
It is the ability of an optical instrument to form a distinct and separable images of the two point objects which are close to each other. If ’ d’ is the least distance between two closer points objects, then
The resolving power \doteq \frac{1}{\mathrm{~d}}=\frac{2 \mathrm{NA}}{\lambda_0}
Where λ0 is the wavelength of the light through vacuum. and NA is the Numerical aperture of the objective of the microscope.
20. State the principle of electron microscope.
In an electron microscope a stream of electrons are passed through the object and the electrons which carry the information about the object are focussed by electric and magnetic lenses (or) electro magnetic lenses.
21. Mention the application of electron microscope.
- It has a very wide area of application in biology, metallurgy, physics, chemistry, medicine, engineering.
- It is used to determine the complicated structure of the crystals.
- It is used in the study of celluloids.
- It is used to study about the structure of micro organisms such as virus, bacteria etc.
22. List out the advantages and disadvantages of SEM.
Advantages
- It can be used to examine specimens of large thickness.
- It has large depth of focus.
- It can be used to get a three dimensional image of the object.
- Since the image can be directly viewed in the screen, structural details can be resolved in a precise manner.
- The magnification may be up to 3,00,000 times greater than that of the size of the object.
Disadvantages
The resolution of the image is limited to about 10-20, hence its resolution is very poor.
23. Mention the applications of scanning electron microscope.
It is used to examine the structure of very large specimens in a three dimensional view.
This microscope also has wide range of applications in various fields such as biology, industries, engineering, physics, chemistry, etc.
| Read More Topics |
| Quantum Physics – Questions and Answers |
| Properties of Matter – Questions and Answers |
| Crystal Physics – Questions and Answers |
