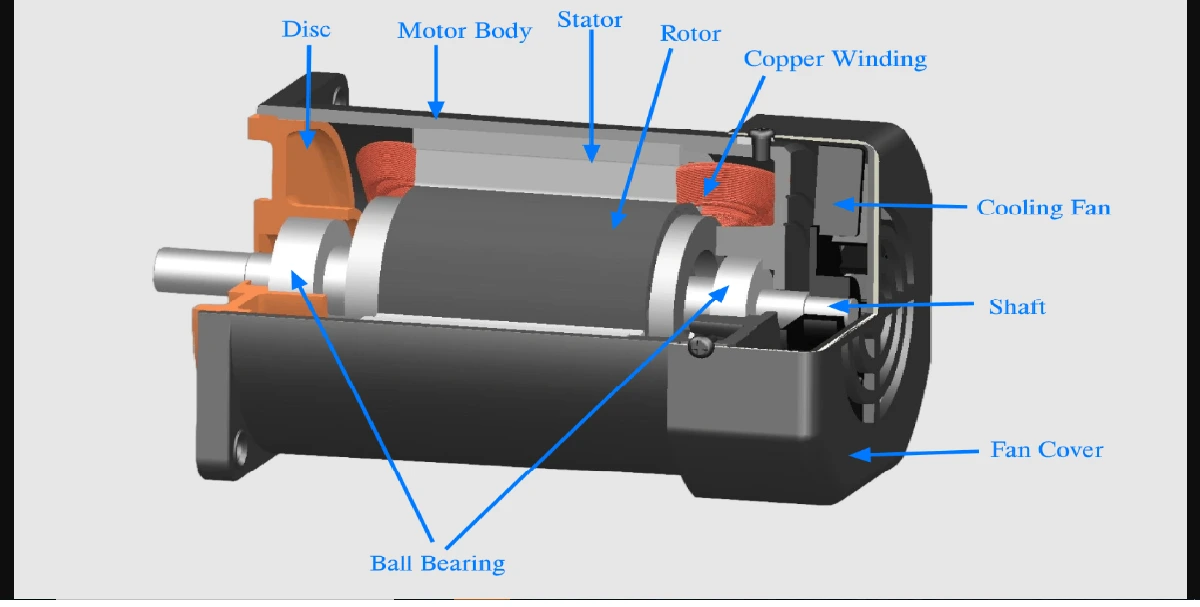
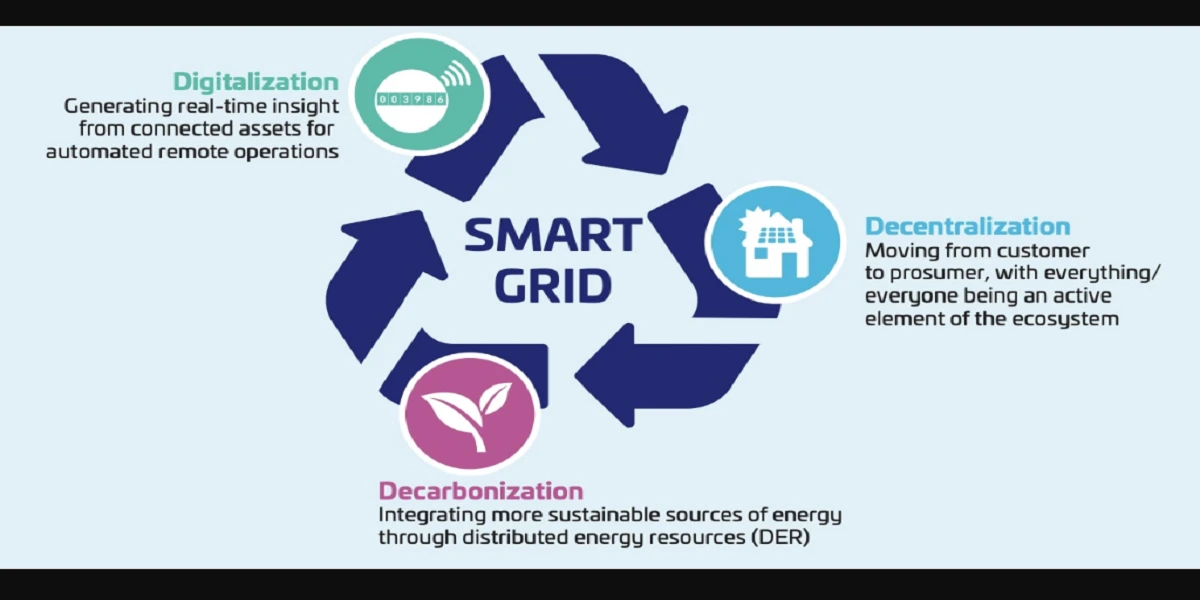
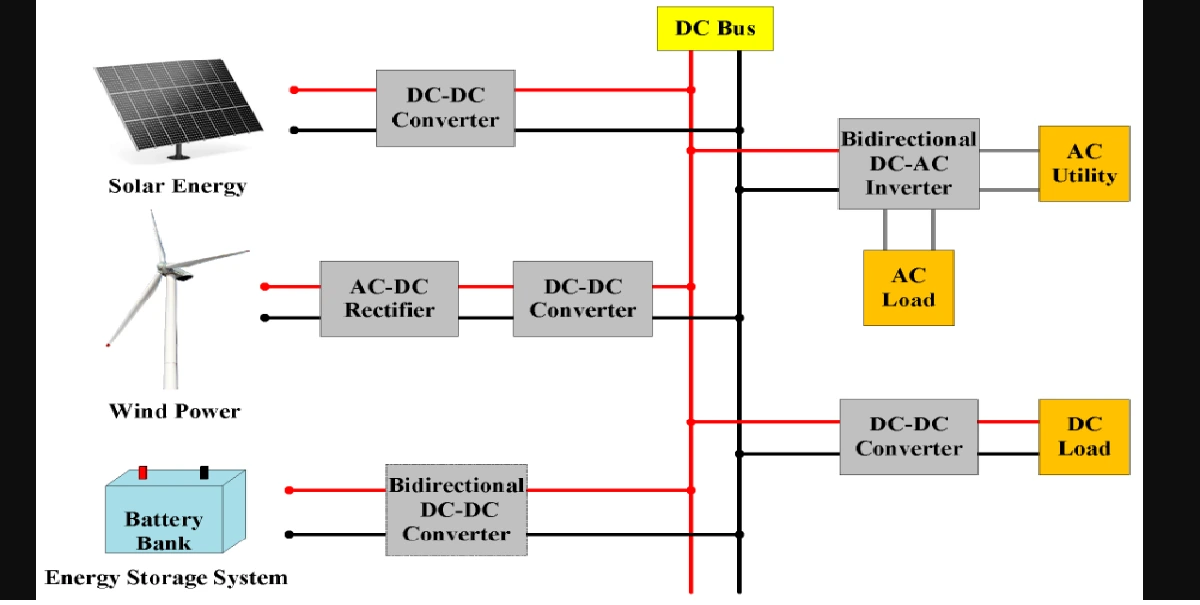
Power engineering deals with highly complex and large-scale systems. From grid networks to transformers, there’s always a need to make things simpler and consistent. That’s where the per unit system steps in like a superhero with a calculator. But what makes it so helpful? Let’s dive into why per unit system simplifies power engineering and why engineers swear by it.
What Is the Per Unit System?
In simple terms, the per unit system expresses electrical quantities as fractions of a defined base unit. Think of it as converting your regular currency into tokens in a game—easier to track, easier to compare.
Brief History and Evolution
The per unit method has been around since the early 20th century. As electrical grids expanded, engineers needed a standardized way to deal with components of different ratings—enter the per unit system.
Where Is It Used in Power Engineering?

You’ll find per unit values everywhere—transmission systems, transformers, load flow analysis, and even in power system protection. It’s the go-to tool when systems have equipment with varied ratings.
The Need for Simplification in Power Engineering
Complexity of Large Power Systems
Modern grids aren’t simple—they’re interconnected webs of voltage levels, generators, transformers, and more. Without simplification, calculations would be chaotic.
Challenges of Varying Voltage and Power Ratings
When every piece of equipment has different ratings, comparing apples to oranges becomes a daily headache. The per unit system brings everything to the same level.
Limitations of Using Actual Values
Actual values change across systems. 1000 A in one system may mean something very different in another. Per unit values remove that ambiguity.
Key Concepts in the Per Unit System
Base Values Explained
Before you can calculate per unit, you need base values for:
Voltage (V_base)
Power (S_base)
Current (I_base)
Impedance (Z_base)
These are the reference points.
How Per Unit Values Are Calculated
Use this simple formula:
Per Unit Value = Actual Value / Base Value
That’s it. Easy, right?
Per Unit Formulas You Should Know
Z_pu = Z_actual / Z_base
V_pu = V_actual / V_base
I_pu = I_actual / I_base
These are your best friends in system modeling.
Why Per Unit System Simplifies Power Engineering
Uniformity Across the System
No matter how big or small the equipment, per unit normalizes everything. That’s like making all currencies the same in a global economy!
Easy Fault Analysis
Short circuits? Voltage drops? Per unit makes fault analysis straightforward by simplifying network equations.
Simplifies Equipment Comparison
Comparing a 220V transformer with a 110kV one is tough. In per unit? Cakewalk.
Minimizes Calculation Errors
Standardization reduces human error. Engineers make fewer mistakes, and results are easier to verify.
System Modeling Made Easy
Software simulations love per unit systems. They’re ideal for load flow studies and transient analysis.
Real-World Applications
Transformers and the Per Unit System
Transformer analysis becomes way easier when you convert impedances to per unit—no need to scale values up or down.
Power Flow Studies
In load flow analysis, per unit values help balance multiple buses and generators effortlessly.
Protection System Coordination
Relays, circuit breakers, and fuses rely on normalized values for accurate performance.
Example Calculations
Step-by-Step Transformer Per Unit Calculation
Choose base values: 100 MVA, 11 kV
Calculate Z_base = (V²) / S = (11²)/100 = 1.21 ohms
If actual impedance is 0.242 ohm, Z_pu = 0.242 / 1.21 = 2 pu
Multi-Voltage Level System Example
Use the same base power but change voltage base per level. Transformers are handled seamlessly using per unit.
Conclusion: So, why per unit system simplifies power engineering? Because it brings clarity, consistency, and ease into a world that’s otherwise full of complexity. From fault analysis to simulation, per unit systems are the unsung heroes behind every stable power network. Whether you’re a student, engineer, or researcher, mastering this system is a game-changer. Normalize your thinking, one per unit at a time!
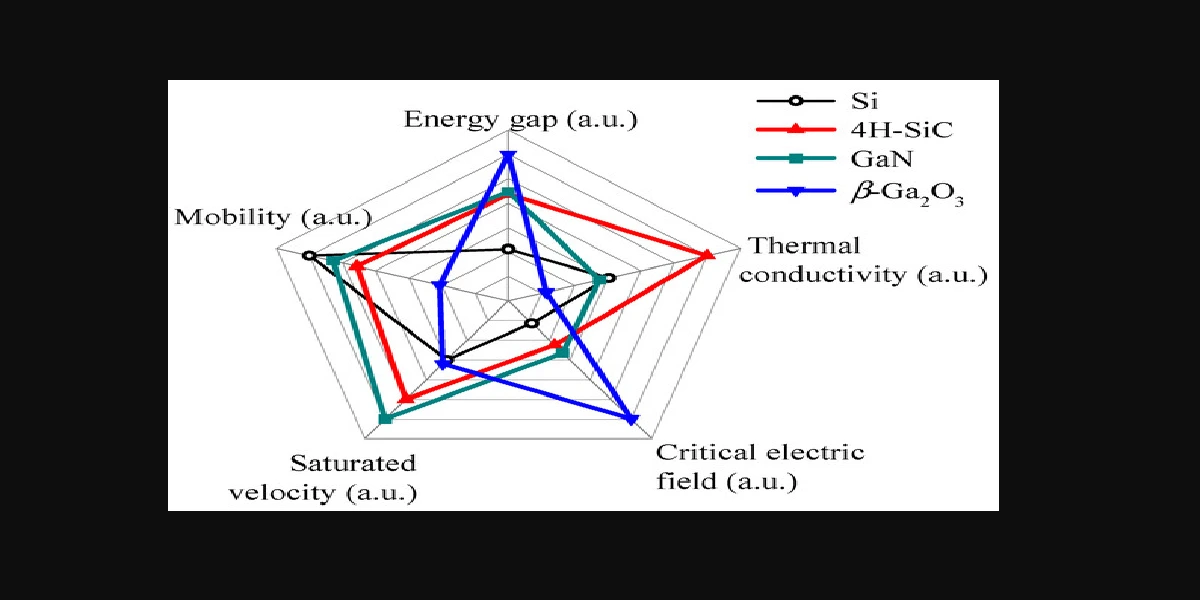
Read also: Wide Bandgap Semiconductors Sic Gan