Classical Free Electron Theory of Metals

Drude – Lorentz Theory

In 1900, Drude was first to explained metallic conduction on the basis of his free electron theory. In 1909, H.A. Lorentz modified this Drude model by applying Maxwell-Boltzmann statistics on the electron gas. This combined idea of Drude and Lorentz is known as Lorentz-Drude theory or classical free electron theory. This theory reveals that the free electrons are fully responsible for electrical conduction.

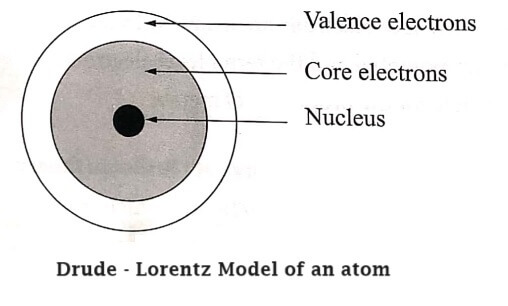
Principle: Classical free electron theory of metals explains the electrical and thermal properties of solids based on classical laws. Generally, an atom consists of central nucleus with positive charge. surrounded by electrons of negative charge as shown in fig Drude assumed that the electrons in a metal are free to move in all directions and form an electron gas. These free electrons move randomly in all possible directions just like the gas molecules in a container.

Postulates of classical free electron theory

(a) In the absence of electric field

1. In an atom electrons revolve around the nucleus.
2. The valence electrons of atoms are free to move about the whole volume of metal like the molecules of a perfect gas in a container.
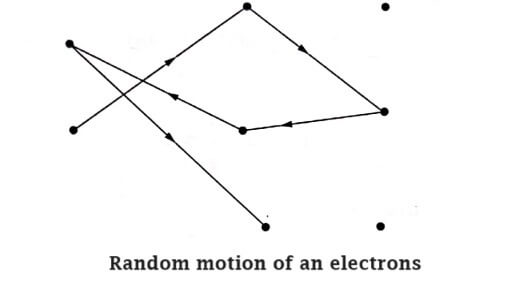
3. In the absence of electric field, these free electrons move in random directions and collide with each other and all the collisions are perfectly elastic.

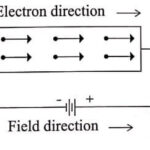
(b) In the presence of electric field

1. Since the electrons are assumed to be perfect gas, they obey the laws of classical kinetic theory of gases.
2. Also the velocity of electrons in a metal obey the Maxwell-Boltzmann statistics.
3. When an electric field (E) is applied to the metal, the free electrons are accelerated in the direction opposite to the direction of applied electric field.

Basic terms involved in the classical free electron theory

(i) Drift velocity (V_d)

The average velocity acquired by the free electron in a particular direction, due to the application of electric field is called drift velocity.

\begin{gathered} \text { Deift velocity }=\frac{\text { average dis tan ce travelled by the electron }}{\text { Time taken }} \\ \qquad v_{d}=\frac{l}{t} \mathrm{~ms}^{-1} \end{gathered}

(ii) Relaxation time (τ)

It is the time taken by the free electron to reach its equilibrium position from its disturbed position, in the presence of applied field.

t=\frac{1}{V_{d}}

where, l is the distance travelled by the electron.

The value of relaxation time is of the order of 10^-14 seconds.

(iii) Collision time (τ_c)

It is the average time taken by a free electron between two successive collision.

\tau_{c}=\frac{\lambda}{V_{d}} \quad \text { where, } \lambda \text { is mean free path. }

(iv) Mean free path (λ)

The average distance travelled between two successive collision is called mean free path.

\lambda=\bar{c} \tau_{c}

where  \bar{c}  is the root mean square velocity of the electron.