Conducting Materials - Solved Problems

1. A uniform silver wire has a resistivity of 1.54 × 10^-8 Ωm at room temperature, for an electrical field along the wire of 1 V/cm. Compute the drift velocity of electron assuming the there are 5.8 × 10²⁸Conducting electrons/m³. Also calculate the mobility.

Given

ρ = 1.54 × 10^-8 Ωm, E = 1 V/cm100 V/m, n=5.8×10²⁸ m^-3, V_d = ?

Solution:-

But V_d = μE

$\begin{aligned} \mu & =\frac{\sigma}{\text { ne }} \\ & =\frac{1}{\rho n \mathrm{e}}\left(\sigma=\frac{1}{\rho}\right) \\ & =\frac{1}{1.54 \times 10^{-8} \times 5.8 \times 10^{28} \times 1.602 \times 10^{-19}} \\ \mu & =6.9 \times 10^{-3} \mathrm{~m}^{2} \mathrm{~V}^{1} \mathrm{~S}^{-1} \\ \mathrm{~V}_{\mathrm{d}} & =\mu \mathrm{E} \\ & =6.9 \times 10^{-3} \times 100 \\ \mathrm{~V}_{\mathrm{d}} & =0.6988 \mathrm{~ms}^{-1} \end{aligned}$

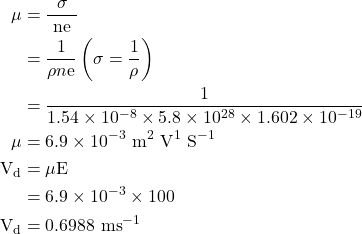
2. The mean free collision time of copper at $300K$ is equal to $2\times10 -14$ sec. Determine its electrical conductivity. Density of electrons is 8.5 $\times10 28 /m³$ .

Given

n=8.5 × 10²⁸ m^-3, τ=2×10^-4 sec, σ=?

Solution:-

$\begin{aligned} \sigma & =\frac{\mathrm{ne}^{2} \tau}{\mathrm{m}} \\ & =\frac{8.5 \times 10^{28} \times\left(1.602 \times 10^{-19}\right)^{2} \times 2 \times 10^{-14}}{9.11 \times 10^{-31}} \\ \sigma & =4.789 \times 10^{7} \mathrm{ohm}^{-1} \mathrm{~m}^{-1} \end{aligned}$

3. Find the relaxation time of conduction electrons in a metal of resistivity $1.54\times10 -8 ohm-m$ if the metal has $5.8\times10 28$ conduction electrons $/m³$ .

Given

ρ = 1.54×10^-8 ohm-m (room temperature), n=5.8×10²⁸ / m³, μ=?, τ=?

Solution:-

$\sigma=\frac{\mathrm{ne}^{\mathrm{e}} \tau}{\mathrm{m}}$

We know $\quad \sigma=\frac{1}{\rho}$

$\begin{aligned} \frac{1}{\rho} & =\frac{\mathrm{ne}^{\mathrm{e}} \tau}{\mathrm{m}} \\ \tau & =\frac{\mathrm{m}}{\mathrm{ne}^{2} \rho} \end{aligned}$

$\begin{aligned} & =\frac{9.11 \times 10^{-31}}{1.54 \times 10^{-8} \times\left(1.02 \times 10^{-19}\right)^{2} \times 5.8 \times 10^{28}} \\ \tau & =3.97 \times 10^{-14} \text { second } \end{aligned}$

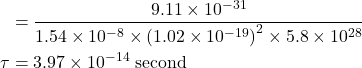
4. The density of silver is $10.5\times10³ kg/m³$ . The atomic weight of silver is $107.9\times10 -3 kg/m³$ . The conductivity of silver at $20°C$ is $6.8\times10 7$ $ohm -1 m -1$ . Assuming that each silver atom contributes one conduction electron calculate (a) the density of electrons and (b) The mobility of electrons in silver.

Given

σ = 6.8× 10⁷ ohm^-1 m^-1, density = 10.5×10³ kg/m³, μ=?, n=?

Solution:-

a. $\mathrm{n}=\frac{\text { Avogadros no } \times \text { density } \times \text { No. of free electrons per atom }}{\text { Atomic weight }}$

$\begin{aligned} & =\frac{6.02 \times 10^{26} \times 10.5 \times 10^{3}}{107.9 \times 10^{-3}} \\ \mathrm{n} & =5.858 \times 10^{31} \text { atoms } / \mathrm{m}^{3} \end{aligned}$

b. σ = neμ

$\mu=\frac{\sigma}{\mathrm{ne}}$

$\begin{aligned} & =\frac{6.8 \times 10^{7}}{6.853 \times 10^{31} \times 1.602 \times 10^{-19}} \\ \mu & =7.245 \times 10^{-3} \mathrm{~m}^{2} \mathrm{v}^{-1} \mathrm{sec}^{-1} \end{aligned}$

5. Evaluate the value of Fermi distribution function for an energy $kT$ above the Fermi energy at that temperature and give some comments on your answer.

Solution:-

Fermi distribution function, $F(E)=\frac{1}{1+\exp \left(\frac{E-E_{F}}{k T}\right)}$

The given energy value, E = E_F + kT

E – E_F = kT

Substituting eqn. (2) in eqn. (1), we get

$\mathrm{F}(\mathrm{E})=\frac{1}{1+\exp (1)}$

$\begin{aligned} & =\frac{1}{1+2.718} \\ \mathrm{~F}(\mathrm{E}) & =0.268 \end{aligned}$

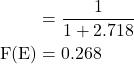
The probability of occupation of electron as that energy is about 0.269. Since the probability is so small, the presence of electrons as that energy level is not certain.

6. Compute the electrical resistivity of Sodium at $0°C$ , if the mean free time at this temperature is $3.1\times10 -14 sec$ . Further more, Sodium builds a B.C.C. lattice with two atoms per unit cell and the side of the unit cell is $0.429 nm$ .

Given : τ=3.1×10^-14 sec, a=0.429×10^-9 m, ρ= ?

Solution:-

Volume of unit cell $a³=(0.429\times10 -9)³ m³$ .

Number of atoms per unit cell = 2

$\begin{aligned} & \therefore=\text { No. of electrons per unit volume, i.e., } \\ & \text { carrier concentration }=\frac{\text { no.of atoms } / \text { unit cell }}{\text { volume of unit cell }} \\ &=\frac{2}{\left(0.429 \times 10^{-9}\right)^{3}} \\ & n=25.33 \times 10^{27} / \mathrm{m}^{3} \end{aligned}$

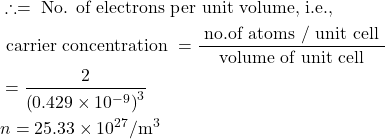
electical conductivity $\sigma=\frac{\mathrm{ne}^{2} \tau}{\mathrm{m}}$

∴ resistivity $\rho=\frac{1}{\sigma}=\frac{\mathrm{m}}{\mathrm{ne}^{2} \tau}$

$\begin{aligned} & =\frac{9.11 \times 10^{-31}}{25.33 \times 10^{27} \times\left(1.602 \times 10^{-19}\right)^{2} \times 3.1 \times 10^{-14}} \\ \rho & =4.52 \times 10^{-8} \Omega-\mathrm{m} \end{aligned}$

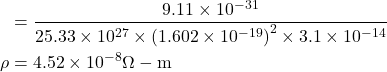
7. Find the temperature at which there is $1%$ probability of a state with an energy $0.5eV$ above Fermi energy.

Given

E = E_F + 0.5 eV; F(E) = 1% = 0.01

Solution:-

$\text { Formula } F(E)=\frac{1}{1+\exp \frac{\left(E-E_{F}\right)}{k T}}$

Hence $\quad 0.01=\frac{1}{1+\exp \left(\frac{0.5}{\mathrm{kT}}\right)}$

$0.01=\exp \left(\frac{0.5}{\mathrm{kT}}\right)=(1-0.01)=0.99$

$\exp \left(\frac{0.5}{\mathrm{kT}}\right)=99$

$\begin{aligned} \frac{0.5}{\mathrm{kT}} & =2.303 \times \log _{10} 99 \\ \mathrm{kT} & =\frac{0.5}{2.303 \times \log _{10} 99} \\ & =0.109 \mathrm{eV} \\ \mathrm{T} & =\frac{0.109 \times 16 \times 10^{-19}}{1.38 \times 10^{-23}} \\ \mathrm{~T} & =1262 \mathrm{~K} \end{aligned}$

8. Calculate the electrical and thermal conductivities for a metal with a relaxation time 10^-14 seconds at 300K. Also calculate the Lorentz number using the above result. (Density of electron n =6×10²⁸ m^-3)

Given

τ=10^-14 sec, T=300 K, n=6×10²⁸ m^-3, σ=? K=?, L=?

Solution:-

$\begin{aligned} \sigma & =\frac{\mathrm{ne}^{2} \tau}{\mathrm{m}} \\ & =\frac{6 \times 10^{28} \times\left(1.602 \times 10^{-19}\right)^{2} \times 10^{-14}}{9.11 \times 10^{-31}} \\ \sigma & =1.690 \times 10^{7} \mathrm{ohm}^{-1} \mathrm{~m}^{-1} \\ \mathrm{k} & =\frac{\pi^{2}}{3}\left(\frac{\mathrm{nk}^{2} \tau}{\mathrm{m}}\right) \mathrm{T} \quad \text { (from Quantum Theory) } \end{aligned}$

$=\frac{(3.14)^{2} \times\left(6 \times 10^{28}\right) \times\left(1.38 \times 10^{-23}\right)^{2} \times 10^{-14} \times 300}{3 \times 9.11 \times 10^{-31}}$

$\begin{aligned} & \mathrm{K}=123.66 \mathrm{Wm}^{-1} \mathrm{~K}^{-1} \\ & \mathrm{~L}=\frac{\mathrm{K}}{\sigma \mathrm{T}} \\ & =\frac{123.66}{1.690 \times 10^{7} \times 300} \\ & \mathrm{~L}=2.439 \times 10^{-8} \mathrm{~W} \Omega \mathrm{K}^{-2} \end{aligned}$

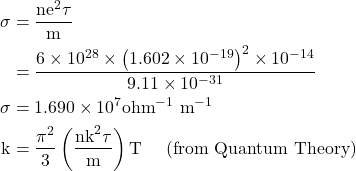
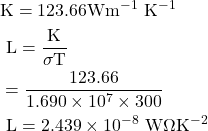
9. Free electron density of aluminium is 18.10×10²⁸ m^-3. Calculate its Fermi energy at 0K. Planck’s constant and mass of free electron are 6.62×10^-34 Js and 9.11×10^-31 kg.

Given

Electron density of aluminium n=18.10×10²⁸ m^-3
Planck’s constant h = 6.62×10^-34 JsMass of electron m = 9.11×10^-31 kg.

Solution:-

Fermi energy at $0 \mathrm{~K} \quad E_{F}=\frac{h^{2}}{2 m}\left(\frac{3 n}{8 \pi}\right)^{\frac{2}{3}}$

Substituting the given values, we have

$\mathrm{E}_{\mathrm{F}}=\frac{\left(6.62 \times 10^{-34}\right)^{2}}{2 \times 9.11 \times 10^{-31}}\left(\frac{3 \times 18.10 \times 10^{28}}{8 \times 3.14}\right)^{\frac{2}{3}}$

E_F = 1.869×10^-18 J

interms of electron volt,

$\begin{aligned} & E_{F}=\frac{1.869 \times 10^{-18}}{1.6 \times 10^{-19}} \mathrm{eV} \\ & E_{F}=11.68 \mathrm{eV} \end{aligned}$

10. The Fermi energy of silver is $5.51eV$ . What is the average energy of a free electron a $0K$ ?

Given

Fermi energy of silver E_F = 5.51 eV

Solution:-

Average (or) mean energy of a free electron at 0K

$\begin{aligned} \mathrm{E}_{\mathrm{ave}} & =\frac{3}{5} \mathrm{E}_{\mathrm{F}} \\ & =\frac{3}{5} \times 5.51 \mathrm{eV} \\ \mathrm{E}_{\mathrm{ave}} & =3.306 \mathrm{eV} \end{aligned}$

Conducting Materials – Solved Problems

Santhakumar Raja

Related Categories

Law

Health science