Three Types of Moduli Elasticity

There are three types of modulus based on different kinds of strain.

They are

Young’s modulus (Y) (corresponding to longitudinal strain)
Bulk modulus (K) (corresponding to volume strain)
Rigidity modulus (N) (corresponding to shear strain)

Young’s modulus (Y)

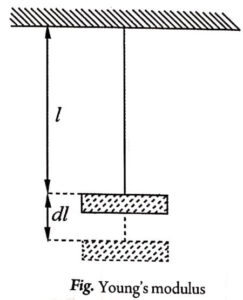
Young’s modulus of the materials of the wire is defined as the ratio of longitudinal stress to longitudinal strain. It is denoted by $Y$ . The unit is N/m²

Consider a wire of length $l$ and area of cross section $A$ to be stretched by a longitudinal force $F$ producing an extension $dl$ (Fig). If $Y$ be the young’s modulus of elasticity, then

\begin{gathered} \text { Longitudinal stress }=\frac{\text { Force }}{\text { Area }}=\frac{\mathrm{F}}{\mathrm{A}} \\ \text { Longitudinal strain }=\frac{\text { change in length }}{\text { original length }}=\frac{\mathrm{d} l}{l} \end{gathered}

∴ Young’s modulus $(\mathrm{Y})=\frac{\text { longitudinal stress }}{\text { longitudial strain }} \quad=\frac{\mathrm{F} / \mathrm{A}}{\mathrm{d} l / l}=\frac{\mathrm{F} l}{\mathrm{Ad} l}$

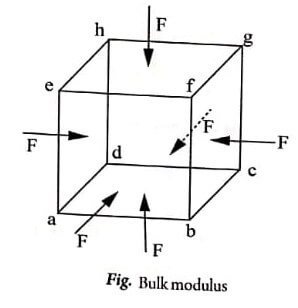
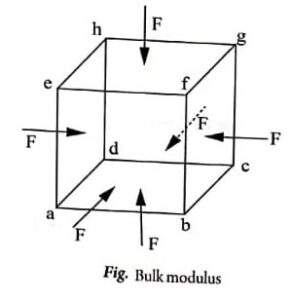
Bulk modulus (K)

Bulk modulus of the material of the object is defined as the ratio of bulk stress to bulk strain. It is denoted by $K$ . The unit is N $/m²$

Consider a body of volume $V$ and area of cross section $A$ as shown in (Fig). Let $F$ be the force applied under normal condition to the whole surface of the body. This results in a change in volume but there is no change in shape of the body. Let $dV$ be the change in volume.

\text { Bulk stress }=\frac{\text { Force }}{\text { Area }}=\frac{\mathrm{F}}{\mathrm{A}}

\text { Bulk strain }=\frac{\text { change in volume }}{\text { original volume }}=\frac{-\mathrm{dV}}{\mathrm{V}}

(The negative sign indicates that volume decreases)

∴ Bulk modulus

\begin{aligned} \mathrm{K} & =\frac{\text { Bulk stress }}{\text { Bulk strain }} \\ \mathrm{K} & =\frac{\mathrm{F} / \mathrm{A}}{-\frac{\mathrm{dV}}{\mathrm{V}}}=\frac{\mathrm{P}}{-\frac{\mathrm{dV}}{\mathrm{V}}} \quad\left[\because \mathrm{P}=\frac{\mathrm{F}}{\mathrm{A}}\right] \\ \mathrm{K} & =\frac{-\mathrm{PV}}{\mathrm{dV}} \end{aligned}

where $P$ is pressure and equal to force per unit area.

The reciprocal of the bulk modulus is called compressibility.

Bulk modulus

Rigidity modulus or shear modulus (N)

Shear modulus or rigidity modulus of the material of the object is defined as the ratio of shear stress to shear strain. It is denoted by $N$ . The unit is $N/m²$

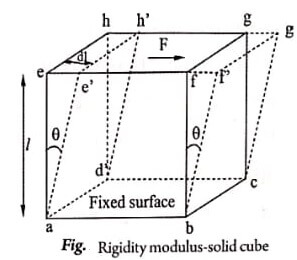
Consider a solid cube subjected to a force in the upper portion, as shown in (Fig). The applied force changes the shape of the body without causing any change in its volume.

Positions of the points like e, $f, g$ and $h$ are shifted respectively, to the points $e', f', g'$ and h’. The face efgh is sheared through an angle θ. The vertical faces turn through an angle θ which gives the shearing strain as,

\text { shearing strain }(\theta)=\frac{\mathrm{ee}^{\prime}}{\text { ae }}=\frac{\mathrm{d} l}{l}

If the area of top surface is $A$ , then, shearing stress $=\frac{F}{A}$

∴ Rigidity modulus $(N)=\frac{\text { shearing stress }}{\text { shearing strain }}$ $=\frac{F / A}{\theta}=\frac{F / A}{\frac{\mathrm{d} l}{l}}$ $\mathrm{N}=\frac{\mathrm{Fl}}{\mathrm{Adl}}$