Since most of the vibrating system follow harmonic motion (SHM), therefore it is essential to have proper understanding of SHM related basic concepts.
A body is said to have simple harmonic motion (SHM), if it moves or vibrates about a mean position such that its acceleration is always proportional to its distance from the mean position and is directed towards the mean position or equilibrium position.
Differential Equation of SHM
Consider a particle ‘P’ moving around a circle with a uniform angular velocity ω rad/s as show in fig.
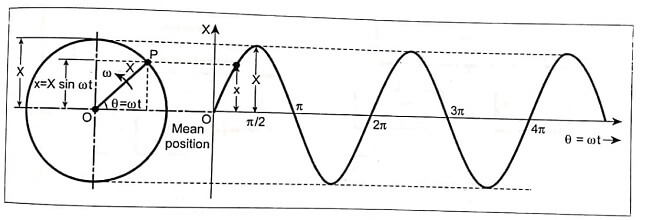
Displacement of particle ‘P’ from mean position after time ‘t’, as shown in fig. is given by
v=\frac{d x}{d t}=\omega \mathrm{X} \cos \omega tAcceleration of particle after time ‘t’ is
\begin{array}{rlr} a=\frac{d^{2} x}{d t^{2}}=-\omega^{2} X \sin \omega t=-\omega^{2} x & \quad[\because x=X \sin \omega t] \\ \qquad \frac{d^{2} x}{d t^{2}}+\omega^{2} x=0 & \end{array}The above equation is known as differential equation or fundamental equation of S.H.M.
Time period and frequency:
Time Period, t_{p}=\frac{2 \pi}{\omega}
Frequency, f=\frac{1}{t_{p}}=\frac{\omega}{2 \pi}
| Read More Topics |
| Fundamentals of vibration |
| Reciprocating pump |
| Types of balancing machine |
