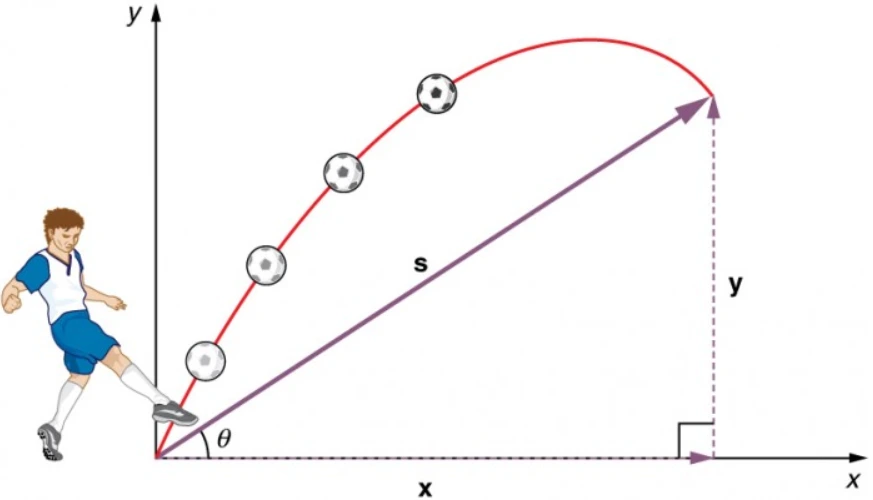
Carrier concentration in metals is the number of electrons N(E) per unit volume in the energy interval E and E + dE.
Each electron energy level can accommodate two electrons as per Pauli’s exclusion principle.
We have,

The actual number of electrons in dE,
![]()
Calculation of density of electrons and Fermi energy at 0K
At T = 0K,
F(E) = 1

Normally,
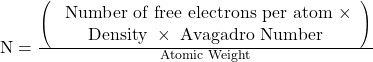
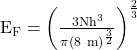
![]()
Hence the Fermi energy of a metal depends only on the density of electrons of that metal.
| Read More Topics |
| Hard and soft magnetic material |
| Basic definitions of magnetic materials |
| Charge densities in a semiconductor |