If N be the number of molecules per unit volume and α the molecular polarizability then
Total polarization \quad \mathrm{P}=\mathrm{N} \alpha \mathrm{E}_{\mathrm{int}}
eqn, (10)
\therefore \quad E_{\text {int }}=\frac{\mathrm{P}}{\mathrm{N} \alpha}Further, we know that
\begin{aligned} \mathrm{D} & =\varepsilon \mathrm{E}=\varepsilon_{0} \mathrm{E}+\mathrm{P} \\ \left(\varepsilon-\varepsilon_{0}\right) \mathrm{E} & =\mathrm{P} \\ \mathrm{E} & =\frac{\mathrm{P}}{\varepsilon-\varepsilon_{0}} \end{aligned}Lorentz field is given by
\mathrm{E}_{\mathrm{int}}=\mathrm{E}+\frac{\mathrm{P}}{3 \varepsilon_{0}}Substituting the value for E, we have
\begin{aligned} & \mathrm{E}_{\text {int }}=\frac{P}{\varepsilon-\varepsilon_{0}}+\frac{P}{3 \varepsilon_{0}} \\ & \mathrm{E}_{\text {int }}=P\left[\frac{3 \varepsilon_{0}+\varepsilon-\varepsilon_{0}}{3 \varepsilon_{0}\left(\varepsilon- varepsilon_{0}\right)}\right] \\ & \mathrm{E}_{\text {int }}=\frac{P}{3 \varepsilon_{0}}\left[\frac{2 \varepsilon_{0}+\varepsilon}{\left(\varepsilon-\varepsilon_{0}\right)}\right] \end{aligned} eqn, (13)Substituting eqn, (10) in (13), we have
\begin{aligned} & \frac{P}{N \alpha}=\frac{P}{3 \varepsilon_{0}}\left(\frac{\varepsilon+2 \varepsilon_{0}}{\varepsilon-\varepsilon_{0}}\right) \\ & \frac{N \alpha}{3 \varepsilon_{0}}=\frac{\varepsilon-\varepsilon_{0}}{\varepsilon+2 \varepsilon_{0}} \end{aligned} =\frac{\left(\frac{\varepsilon}{\varepsilon_{0}}\right)-1}{\left(\frac{\varepsilon}{\varepsilon_{0}}\right)+2} \frac{\mathrm{N} \alpha}{3 \varepsilon_{0}}=\frac{\varepsilon_{\mathrm{r}}-1}{\varepsilon_{\mathrm{r}}+2} \quad \ldots(14) \quad\left[\therefore \varepsilon_{\mathrm{r}}=\frac{\varepsilon}{\varepsilon_{0}}\right]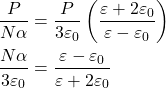The above equation is Clausius – Mosotti relation, which relates the dielectric constant of the material and polarizability. Thus, it relates macroscopic quantity dielectric constant with microscopic quantity polarizability.
| Read More Topics |
| Internal field or local field |
| Frequency and temperature dependance of polarization |
| Classification of dielectric materials |
