1. What is a conducting material?
Metals are good conductors due to the absence of energy gap and the presence of free electrons with low resistivity.
2. Define drift velocity of electrons.
Drift velocity (Vd) is the velocity acquired by an electron in a perpendicular direction due to the application of electric field.
3. Define mobility of electrons.
It is the drift velocity per unit electric field, \mu=\frac{V_{d}}{E}
4. Define mean free path.
It is the average distance travelled by an electron between two successive collisions in the presence of electric field.
5. Define Mean Collision time (tc)?
It is the time taken by the electron between two successive collisions.
6. Define relaxation time.
Relaxation time (τ) is the time taken by the electron to reach equilibrium position from its disturbed position in the presence of electric field. It is approximately is equal to 10-14 sec.
7. Define electrical conductivity.
The electrical conductivity is defined as the quantity of electricity flowing per unit area per unit time at a constant potential gradient.
8. Define Thermal Conductivity.
Thermal conductivity of material is defined as the amount of heat flowing through an unit area of a material per unit temperature gradient.
9. State Widemann-Franz law.
It states that the ratio of thermal conductivity to electrical conductivity is constant at all temperatures. \frac{K}{\sigma T}=a constant.
10. Mention any four postulates of classical free electron theory.
- A solid metal has nucleus with revolving electrons.
- The électrons move freely like molecules in a gas.
- The free electrons in a metal are moving in a uniform potential field due to fixed ions.
- In the absence of electric field (E=0), the electrons have random collisions called elastic collisions (no loss of energy) and in the presence of electric field (E≠0), the free electrons are accelerated opposite to the applied electric field.
11. What are the Sources of resistance in metals?
- Presence of impurities in the metals
- Temperature of the metal
- Number of free electrons.
12. What is the effect of temperature on metals?
When temperature of the metal increases, the mobility of the electron decreases and hence the electrical conductivity decreases. The addition of impurities in the metal decreases the electrical conductivity.
13. What are the uses of classical free electron theory?
- It is used to verify the Ohm’s law.
- It is used to explain electrical conductivity (σ) and thermal conductivity (K) of metals.
- It is used to derive Widemann-Franz law.
- It is used to explain the optical properties of metal.
14. What are the drawbacks of classical free electron theory?
- There is a difference in theoretical and experimental values of specific heat of metals and electronic specific heat of metals.
- It cannot explain the electrical conductivity (σ) of semiconductors and insulators.
- As per classical theory is constant at all temperatures. But at low temperature is not a constant.
- The theoretical paramagnetic susceptibility (χ) is greater than the experimental value.
- Photoelectric effect, Compton effect and Black body radiation phenomenons cannot be explained by this theory.
15. What is Lorentz Number?
Lorentz number \mathrm{L}=\frac{3 \mathrm{~K}^{2}}{2 \mathrm{e}^{2}} \begin{aligned} \mathrm{L} & =\frac{3 \times\left(1.38 \times 10^{-23}\right)^{2}}{2 \times\left(1.69 \times 10^{-19}\right)^{2}} \\ \mathrm{~L} & =1.12 \times 10^{-8} \quad \mathrm{~W} \Omega \mathrm{K}^{-2} \end{aligned}
It is found that the classical value of Lorentz number is only one half of the experimental value (2.44×10-8 ). The discrepancy of L value is the failure of the classical theory. This can be rectified by quantum theory.
16. What is the basic assumption of Zone theory or Band theory of solids ?
According to quantum free electron theory, the electrons in a metal were assumed to be moving in a region of constant potential but it fails to explain why some solids behave as conductors, some as insulators and some as semiconductors.
Therefore instead of considering an electron to move in a constant potential, the Zone theory of solids tells that the electrons are assumed to move in a field of periodic potential.
17. Define Fermi level and Fermi energy with its importance.
Fermi level: The Fermi level is the highest reference energy level of a particle at absolute zero.
Importance: It is the reference energy level which separates the filled energy levels and vacant energy levels.
Fermi energy [EF]: It is the maximum energy of the quantum state corresponding to Fermi energy level at absolute zero.
Importance: Fermi energy determines the energy of the particle at any temperature.
18. Define Fermi Distribution function.
It is an expression for the distribution of electrons among the energy levels as a function of temperature and it is the probability of finding an electron in a particular energy state of energy E is given by,
F(E)=\frac{1}{1+\exp \left(\frac{E-E_{F}}{K T}\right)}and T= Absolute temperature
19. Draw the Fermi distribution curve at 0 K and at any temperature TK [or] How does the Fermi function varies with temperature.
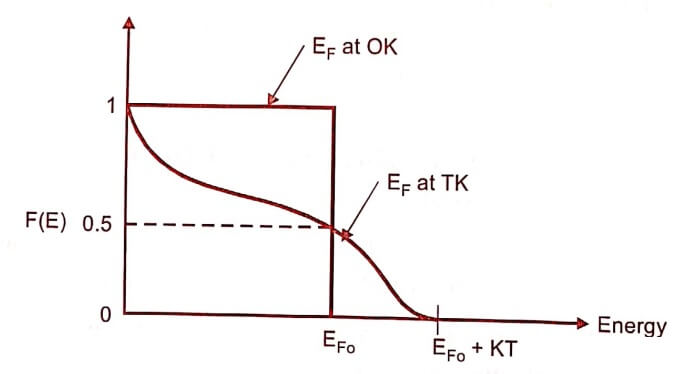
The Fermi function varies with respect to the temperature. At OK all the energy states below EF are filled and all those above it are empty. When the temperature is increased, the electron takes an energy KT and hence the Fermi function falls to zero.
20. Define density of states.
Density of states is defined the as the number of energy states per unit volume in an energy interval of a metal. It is use to calculate the number of charge carriers per unit volume of any solid
\mathrm{D}(\mathrm{E}) \mathrm{dE}=\frac{\text { Number of energy states between }}{\text { Volume of the metal }}21. Give the microscopic form of ohm’s law in a metallic conductor. Whether the Ohm’s law is true at all temperatures.
J = σE , This Ohm’s law is not true at all temperatures in a conductor, since the resistance of a conductor varies with temperature in a complicated manner at different range of temperatures.
22. Define effective mass of electron.
It is the mass of the electron when it is moving through the crystal under the influence of electric or magnetic field. It is denoted by m*. ie., m is not equal to m*.
23. State the relation between thermal conductivity and electrical conductivity. Does it hold good for all types of materials.
\mathrm{K} / \sigma=\mathrm{LT} ,where L is constant called Lorentz number and T is the number of metal in Kelvin. This relation is hold only for metals. At low temperatures this relation is not true even for metals.24. Define drift velocity. How is it different from thermal velocity of an electron?
The drift velocity is defined as the average velocity acquired by an electron due to the application electric field.
The thermal velocity is random and high (105 m/s) but the drift velocity is directional and very small (50 cm/s).
