Isomers resulting from different arrangements of the atoms in space due to the rotation of groups around C-C bond axis are known as conformational isomers. The study of these confirmations or conformational isomers is known as conformational analysis which involves analysis of the shapes that molecules can adopt by rotation about single bond.
Conformations or conformational isomers are different relative arrangements of atoms that can be converted into one another by rotation around single bonds. For example, conformations of lower alkane (ethane and butane); these alkanes are characterised by sigma bonds (single covalent bond) which allow free rotation about its axis due to symmetrical electron distribution of the sigma molecular orbital. This free rotation, results to different elative arrangements (or conformations) of their atoms (alkane) in space that can be interchanged into one another.
Conformational Analysis
Analysis of different shapes that a molecule can adopt as a result of single bond rotation is referred as conformational analysis. A molecule can adopt equilibrium between various shapes. The relative abundance of these shapes is determined by the Boltzmann distribution and that in turn is simply determined by the relative free energy of each shape.
Conformational analysis determines shape related properties of a molecule, like free energy and reactivity. Thus it can be concluded that shape of a molecule is not a static but is a dynamic equilibrium between numbers of conformations. The conformation having lower free energies among all existing shapes, is preferred to represent that specific molecule.
Conformational analysis can be studied under two parts:
Thermodynamic Part: It is analysis of reason behind the preferred conformations adopt the shapes that they do. This concentrates on the free energies ΔG = -RT Ln Keq
Where,
R = Gas constant (1.98 cal/mol per K)
T = Temperature
Keq = Equilibrium constant (between any two conformations differing in free energy by ΔG)
Kinetic Part: It concentrates on reactivity and depends on the free energy of activation Ln(k/T) = 23.76 − ΔG/RT gives the rate (of a unimolecular) reaction. reaction.
Where, ΔG= Free energy barrier for the process
k = Rate constant (in s-1)
Conformational Isomerism of Ethane
In the ethane by the rotation of two tetrahedral methyl groups about the C−C bond axis various arrangements are obtained. The two important arrangements of ethane (i.e., eclipsed and staggered arrangements) are represented by ball-and-stick models as given in figure.
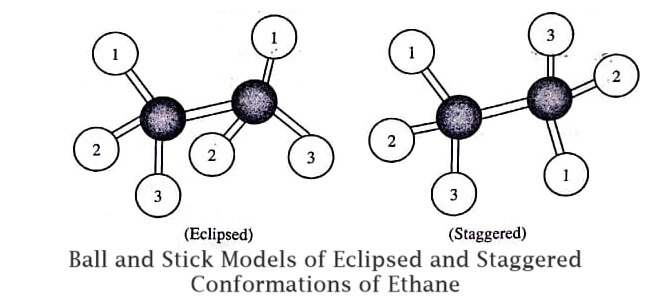
In ethane molecule, carbon-carbon single bond is present and each carbon atom is further attached to three hydrogen atoms.
In all conformations, the bond lengths and the bond angles are specific for the ethane molecule and remain same for it. Among the various possible conformations of ethane, the two conformations (or forms) representing the two extreme are given in figure.
In ethane molecule, the two tetrahedral Same. methyl groups can rotate about the C−C bond axis and give several arrangements (figure):
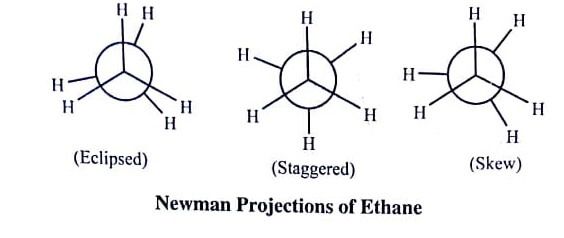
Eclipsed Form: In eclipsed form, the rear methyl group is completely eclipsed and only the nearer methyl group is visible from eyes.
Staggered Form: In this form, the rear methyl group has been rotated upside down and all the six hydrogen atoms of the two methyl groups are staggered symmetrically.
Skew Form: In between the eclipsed form and staggered form many other arrangements are possible. Skew form is representing such arrangements laying anywhere between the two extreme forms.
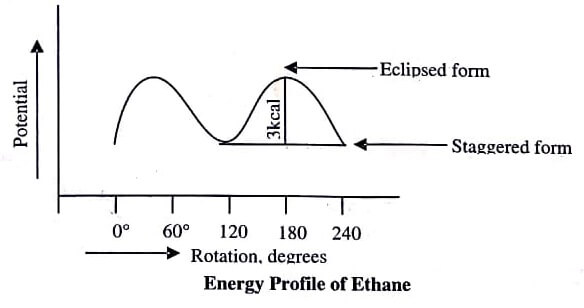
Energy profile of ethane molecule is given in figure:
Melvin Newman suggested that in ethane the front carbon is represented by the intersection of bonds from it, whereas the rear carbon is represented in the form of circle, as shown in figure.
The Newman projection formulas for the conformations of ethane can be given as (figure);
Conformational Isomerism of n-Butane
Two different conformations are possible in n-Butane, one in which methyl group is eclipsed by a methyl group and the second one in which the methyl group is eclipsed by hydrogen (figure). Of these two eclipsed conformations, the one conformation have larger methyl groups eclipsing (I), will naturally experience more repulsive forces than the conformation having a methyl group facing with a H-atom (II). Thus, from stability standpoint, conformation (II) will be preferred.
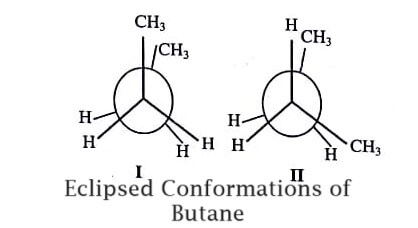
Similarly, it is observed that for butane two different staggered conformations are possible (figure).
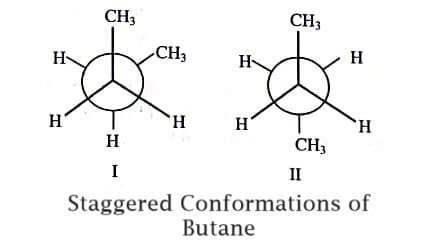
In (I) the methyl groups are at an angle of 60∘ to each other and the conformation is known as Gauche Conformation. In (II) the methyl groups are at an angle of 180∘ to each other and this position is known as Anti- or Trans-Conformation. Due to the proximity of the methyl groups in position (I), the repulsive forces will be greater in (I) than in position (II).
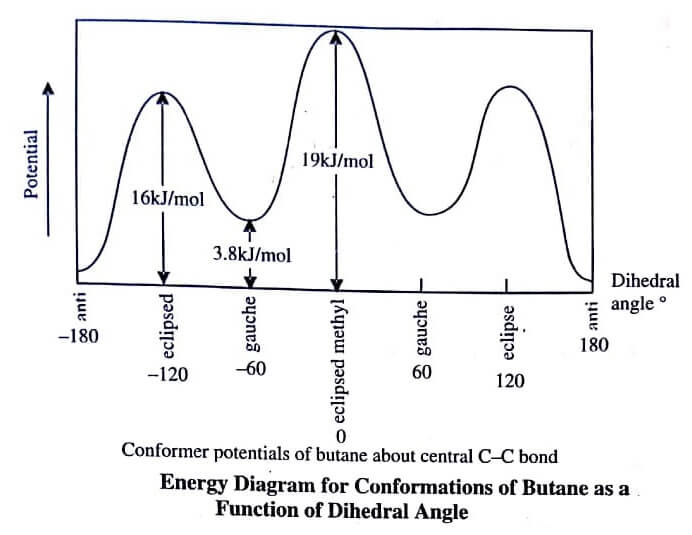
Subsequently, the conformation (II) is associated with least energy and maximum stability. The resulting energy profile of butane is shown in figure.
Conformations of Cyclohexane
The cyclohexane conformation is any of various 3D shapes that a cyclohexane molecule can adopt though maintaining the integrity of its chemical bonds.
The internal angles of a flat regular hexagon are 120°, but the favoured angle between successive bonds in carbon chain is around 109°, i.e., the tetrahedral angle. Thus, the cyclohexane ring adopts non-planar (warped) conformations that have all angles closer to 109°, and therefore lower strain energy than the flat hexagonal shape. The most significant conformations are known as chair, half-chair, boat, and twist-boat.
The molecules easily switch between these conformations and only two of them, i.e., chair and twist-boat can be isolated in pure form:
Chair Conformation: The chair conformations are most stable because the two chair conformations have the lowest total energy. In the basic chair conformation, the carbons C1 through C6 alternate between two parallel planes, i.e., one with C1, C3 and C5, and the other with C2, C4 and C6. The symmetry axis of these molecules is perpendicular to these two planes and is congruent with others after a rotation of 120° about that axis.
The two chair conformations have the same shape and one is similar to other after the rotation of 60° about that axis, or after being mirrored across the mean plane. The perpendicular projection of the ring onto its mean plane is regular hexagon. All C−C bonds are tilted relative to the mean plane, while the opposite bonds (like C1−C2 and C4−C5 ) are parallel to each other.
As a result of the ring warping, six of the 12 carbon-hydrogen bonds end up almost perpendicular to the mean plane. These six carbon-hydrogen bonds are almost parallel to the symmetry axis, with alternating directions, and are said to be axial.
Other six C−H bonds present almost parallel arrangement to the mean plane and are called as equatorial.
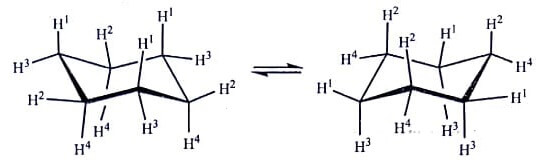
Thus, the precise angles are the two C−H bonds in each carbon (one axial and one equatorial) point in opposite senses relative to the axis of symmetry. So, in a chair conformation, these are three C−H bonds of each kind, i.e., axial “up”, axial “down”, equatorial “up” and equatorial “down”.
Thus each carbon has one “up” and one “down”, and one axial and one equatorial. The hydrogen atoms in successive carbons are therefore staggered and responsible for small torsional strain. Most of the time, this geometry remain same when the hydrogen atoms are replaced by some simple groups like halogens.
The inter-conversion from one chair conformation to other is known as chair-flipping or ring-flipping. During this the carbon-hydrogen bonds that are axial in one configuration become equatorial in the other, and vice versa; but their “up” or “down” properties remain the constant.
In cyclohexane molecule, the two-chair conformations have equal amount of energy. At room temperature, 99.99% of all molecules in cyclohexane solution will be in a chair conformation.
In the derivatives of cyclohexane, the two-chair conformations may have different amount of energy that depends on the identity and position of the substituents. For example, in methylcyclohexane, the lowest energy conformation is a chair in which the methyl group is in equatorial position.
This configuration is responsible for decreased interaction between the methyl group (present on C1) and the hydrogen atoms present at C3 and C5. It avoids the interaction of two gauche butane (of the Cl−CH3 bond with the C2−C3 and C5−C6 ring bonds). Similarly, cis-1,3-dimethylcyclohexane normally has both methyl groups on the equatorial position that avoid the interaction between them. In six-membered heterocyclic compounds (e.g., pyran), a substituent next to a heteroatom may prefer the axial position due to the anomeric effects.
The preference of a substituent towards the equatorial conformation is based on the difference between the Gibbs free energy (A) of two-chair conformations, having substituent in equatorial or in axial position. Positive value of A indicates preferred equatorial position. The magnitude of the A values is ranging between nearly zero (for very small substituents like deuterium), to about 5kcal/mole (for very bulky substituents like tert-butyl group).
Boat Conformation: In the basic boat conformation, carbon atoms at 2, 3, 5 and 6 positions are coplanar, while carbon atoms at position 1 and 4 are displaced away from that plane in the same direction. Therefore, bonds C2− C3 and C5-C6 are parallel. In this conformation, the molecule has two perpendicular planes of symmetry as well as a C2 axis. Energy of the boat conformations is higher than the chair conformations.
In a molecule, interaction between the two flagpole hydrogen-atoms generates steric strain. It is also torsional strain that involves the C2−C3 and C5−C6 bonds that are eclipsed. This is the reason why the boat configuration is unstable (not a local minimum of the energy function).
Twist-Boat Conformation: Twist-boat conformation is also known as twist (D2 symmetry). The twist-boat conformation can be derived from the boat conformation by applying a slight twist to the molecule about the axis connecting the two unique carbons. It results to a structure that has three C2 axis and no plane of symmetry.
At room temperature, the twist-boat conformation exists at very low concentration but at 1073 Kelvin, the concentration may reach to 30%. Rapid cooling from 1073 K to 40 K will freeze in a large concentration of twist-boat conformation, and on heating it may slowly converted to the chair conformation.
Half-Chair Conformation: The half-chair conformation is a transitional shape with C2 symmetry. It is normally considered to be on the pathway between chair and twist-boat. It includes rotation of one of the dihedrals to zero like that of four adjacent atoms are coplanar and the other two atoms are out of the plane (one above and one below).
| Read More Topics |
| Nomenclature of geometrical isomers |
| Types of optical isomerism |
| Photolytic degradation and its prevention |
