Dalton's Law of Partial Pressures

The ideal gas equation establishes the relationship among the pressure exerted by a certain number of moles of a gas, its temperature and the volume occupied by it. But the pressure exerted by a mixture of gases present in a container was studied by Dalton. Dalton’s law states that “the total pressure exerted by a mixture of non-reacting gases taken in a container at a given temperature is the sum of the practical pressures of the individual gases that each gas would exert if it were taken alone in that container. This statement is known as Dalton’s law of partial pressure.

Partial pressure is the pressure exerted by each constituent of the gaseous mixture when they are kept individually in the same container.

If the partial pressures of the constituents of the gaseous mixture are $p 1,p 2,p 3 \dots\dots$ and so on, then according to Dalton’s law of partial pressures, the total pressure $p=p 1,p 2,p 3$

If $n 1$ is the number of moles of a constituent of the gaseous mixture take in a container of volume $V$ and $p 1$ is the pressure exerted by it at temperature $T$ , then

P_{1}=n_{1} \times \frac{R T}{V} \quad \text { (1) (from the ideal gas equation) }

Similarly, if $P$ is the total pressure exerted by the gaseous mixture at temperature $T$ , and $n$ is the total number of moles take in the container of volume V, then RT

eqn (2)

\mathrm{P}=\mathrm{n} \frac{\mathrm{RT}}{\mathrm{V}}

Dividing equation (1) by equation (2), we obtain

\begin{aligned} \frac{\mathrm{p}_{1}}{\mathrm{p}} & =\frac{\mathrm{n}_{1}}{\mathrm{n}} \\ \therefore \quad \mathrm{p}_{1} & =\frac{\mathrm{n}_{1}}{\mathrm{n}} \times \mathrm{P} \end{aligned}

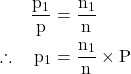
∴ Partial pressure $(p 1)=$ Mole fraction $(n 1 /n) \times$ total pressure of the gas $(P)$

Mole fraction is the ratio of number of moles of an individual gas to the total number of moles of all gases in a mixture.

Dalton’s law of partial pressure is not applicable to gaseous mixture in which the component gases react with each other chemically.

Example: It is not applicable to a mixture of carbon monoxide and oxygen which react with each other to form carbon dioxide at ordinary temperature:

2CO + O₂ → 2CO₂

Read More Topics

Ohm’s law – Physics

Fleming’s right hand rule

Weber – Fechner law