The electrical conductivity is defined as the rate of electric charges flows across a unit area in a unit time per in a conductor per unit potential gradient (or) electric field. It is denoted by σ.

Expression for electrical conductivity
In order to calculate the conductivity of a metal on the basis of classical theory, let us consider a metallic rod subjected to an electric field ‘E’.
When an electric field (E) is applied to a conductor, the free electrons are accelerated and give rise to current (I) which flows in the opposite direction of electric field. The flow of charges is given in terms of current density (J).
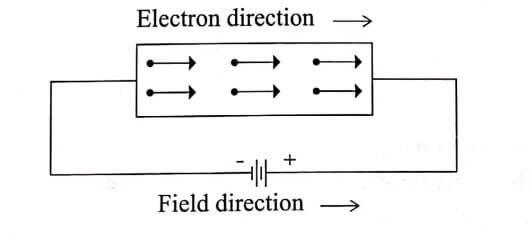
The electrons are accelerated with a drift velocity vd in a direction opposite to that of the applied field.
In an ordinary conductor, the current density is proportional to the applied electric field.
Equation – 1
J α E
J = σE
where σ is the “proportionality constant” called as electrical conductivity of a conductor.
Due to the applied electric field, the electrons acquire an acceleration ‘a’ can be given by
Equation – 2

When an electric field of strength (E) is applied to the conductor, the force experienced by the free electrons is given by
Equation – 3
F = -eE
where, ‘ e ‘ is the charge of a free electron.
Due to this force, the free electrons will acquire an acceleration ‘a’.
From Newton’s second law of motion, the force acquired by the electrons can be written as
Equation – 4
F = ma
Equating (3) and (4)
-eE = ma
Equation – 5
![]()
Now, substituting the value of ‘a’ from eqn. (2) in eqn. (5), we get
Equation – 6
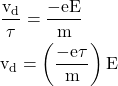
The current density (current per unit area per unit time) is determined by the number of charge carriers and its drift velocity.
Equation – 7
J = n(-e)vd
Substituting eqn. (6) in eqn. (7), we get
Equation – 8

Comparing eqn. (8) and eqn. (1), we get

This is the expression for electrical conductivity.
Conclusion
- Thus, the electrical conductivity is directly proportional to relaxation time of the electrons.
- From this equation we find that with the increase of electron concentration (n), the conductivity (σ) increases.