The sum of the moments of all the forces across the areas of all the filaments about the neutral axis, when a beam is bent is called the bending moment.
When the beam is in equilibrium position the bending moment will be equal to the restoring couple or the moment of resistance of the bending.
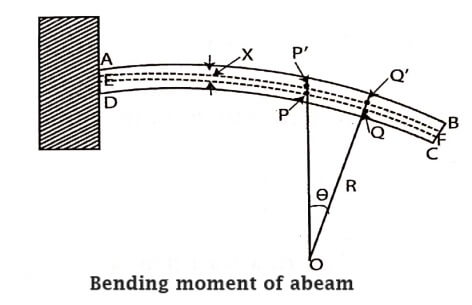
To find an expression for the bending moment consider a small part of the beam bent into a circular arc subtending an angle θ at the centre of curvature O. Let R be the radius of curvature of this part PQ of the neutral axis (Fig). Let P’Q’ be another filament at a distance x from the neutral axis. In the unstrained position of the beam, the length of the fibre PQ=P’Q’=Rθ
In the strained position P’Q’ = (R+x)θ
Strain in the fibre \mathrm{P}^{\prime} \mathrm{Q}^{\prime}=\frac{\text { change in length }}{\text { original length }} \text { Strain }=\frac{(\mathrm{R}+x) \theta-\mathrm{R} \theta}{\mathrm{R} \theta}=\frac{x}{\mathrm{R}}
This shows that the strain is proportional to the distance from the neutral axis.
\begin{aligned} \therefore \text { Youngs' Modulus } Y & =\frac{\text { stress }}{\text { strain }} \\ \text { stress } & =\text { Y.strain } \end{aligned} \text { We know stress }=\text { Y.strain }=\mathrm{Y} \cdot \frac{x}{\mathrm{R}}Let ‘a’ be the area of cross section of the beam, then
\text { stress }=\frac{\text { Force }}{\text { Area }}Force applied on the area ‘a’ is written as
\mathrm{F}=\mathrm{Y} \cdot \frac{x}{\mathrm{R}} \mathrm{a}∴ The moment of the force about \mathrm{EF}=\left[\mathrm{Y}\left(\frac{x}{\mathrm{R}}\right) \mathrm{a}\right] x =\mathrm{Y} \cdot \mathrm{a} \cdot \frac{x^{2}}{\mathrm{R}}
Since the moment of the forces acting on both the upper and lower halves of the section are in the same direction, the total moment of the forces acting on the filaments due to the strain will be
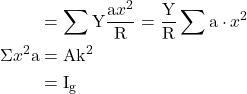
\begin{aligned} & =\sum \mathrm{Y} \frac{\mathrm{a} x^{2}}{\mathrm{R}}=\frac{\mathrm{Y}}{\mathrm{R}} \sum \mathrm{a} \cdot x^{2} \\ \Sigma x^{2} \mathrm{a} & =\mathrm{Ak}^{2} \\ & =\mathrm{I}_{\mathrm{g}} \end{aligned}where A is the total area of cross section of the beam
K is the radius of gyration and
AK² = Ig is the geometric moment of inertia of the beam
\begin{aligned} & \therefore \text { The moment of force } \quad=\frac{\mathrm{Y}}{\mathrm{R}} \cdot \mathrm{I}_{\mathrm{g}} \\ & \therefore \text { Bending moment of the beam }=\frac{\mathrm{Y}}{\mathrm{R}} \cdot \mathrm{I}_{\mathrm{g}} \end{aligned}The quantity Y.Ig(=Y⋅Ak²) is known as flexural rigidity of the beam. It is defined as the bending moment of the beam which produces unit of radius of curvature.
| Read More Topics |
| Poisson’s Ratio (σ) |
| Factors affecting elasticity |
| Three types of moduli elasticity |
