- It is an expression for the distribution of electrons among the energy levels as a function of temperature.
- The probability of finding an electron in a particular energy state of energy E is given by,
Where, EF − Fermi energy (highest energy level of an electron)
K – Boltzmann’s constant
T – Absolute temperature
Effect of Temperature on Fermi Function
Case 1: At T=0 K and E< EF
\begin{array}{ll} \mathrm{F}(\mathrm{E})=\frac{1}{1+\exp (-\infty)}=\frac{1}{1+0} & \left\lvert\, \begin{array}{l} \mathrm{e}^{0}=1 \\ \mathrm{e}^{-\infty}=0 \\ \mathrm{e}=\infty \end{array}\right. \\ \mathrm{F}(\mathrm{E})=1=100 \% & \end{array}- It means that 100% chance to find the particle [electron]
- At zero Kelvin, all energy states below EF are occupied by electrons.
Case 2: At T=0 K and E>EF
- It means that 0% chance to find the particle [electron]
- At zero Kelvin, all energy states above EF are empty.
Case 3: At T>0 K and E=EF
\begin{aligned} & F(E)=\frac{1}{1+\exp (0)}=\frac{1}{1+1}=\frac{1}{2}=0.5 \\ & F(E)=0.5=50 \% \end{aligned}- It means that 50% chance to find the particle [electron]
- At zero Kelvin, energy states above EF are empty and below EF are filled.
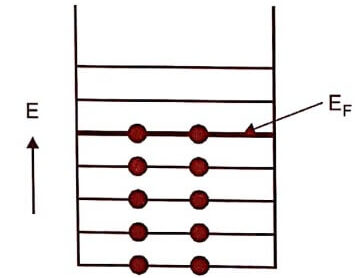
Fig 1.1
Where EF is Fermi energy or Fermi Level.
Fermi level : The Fermi level is the highest reference energy level of a particle at absolute zero.
Importance : It is the reference energy level which separates the filled energy levels and vacant energy levels.
Fermi energy [EF ] : It is the maximum energy of the quantum state corresponding to Fermi energy level at absolute zero.
Importance : Fermi energy determines the energy of the particle at any temperature.
Variation of Fermi function with temperature
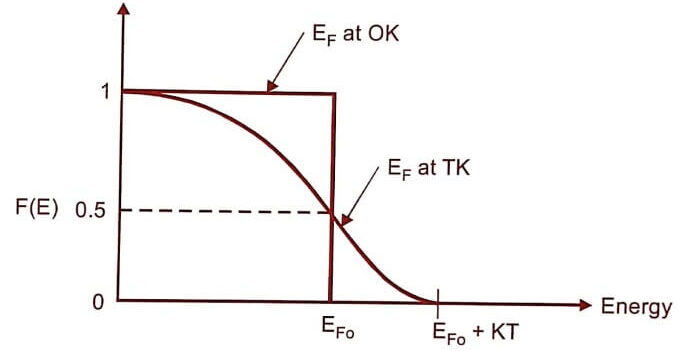
When the temperature is increased, the electron takes an energy KT and hence the Fermi function falls to zero.
| Read More Topics |
| Energy distribution of electrons in metals |
| Three types of optical fibre |
| Fibre – Optic sensor working principle |
