Linear Flow of Heat Along a Bar

The heat which is flowing along the length of the bar (linearly) is called linear heat flow or rectilinear heat flow.

Let us consider a long metal bar heated at one end and let us consider the flow of heat along x-axis as shown in (Fig. 1).

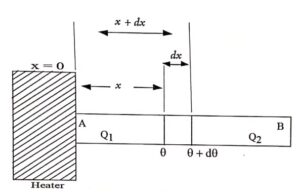
Fig. (1) Flow of heat along a bar

Let us consider two parallel planes perpendicular to the x axis and at a distance x and x $+δx$ from the hot end. Let $θ$ be the excess of temperature at the plane x and $\frac{\mathrm{d} \theta}{\mathrm{d} x}$ be the temperature gradient.

Then the excess of temperature at the plane x

+δx

will be

(θ+ \frac{\mathrm{d} \theta}{\mathrm{d} x} .δx)

and the temperature gradient will be

\frac{\mathrm{d} \theta}{\mathrm{d} x}

((θ+ \frac{\mathrm{d} \theta}{\mathrm{d} x} .δx))

If Q₁ and Q₂ be the quantities of heat that enter the plane at x and leave the plane at

(x+δx)/

sec respectively, we have

eqn (1)

\mathrm{Q}_{1}=-\mathrm{KA} \frac{\mathrm{d} \theta}{\mathrm{d} x}

where $K$ is the coefficient of thermal conductivity and $A$ is the area of cross section of the bar.

Therefore,

eqn (2)

\begin{aligned} \mathrm{Q}_{2} & =-\mathrm{KA} \frac{\mathrm{d}}{\mathrm{d} x}\left(\theta+\frac{\mathrm{d} \theta}{\mathrm{d} x} \cdot \delta x\right) \\ & =-\mathrm{KA}\left[\frac{\mathrm{d} \theta}{\mathrm{d} x}+\frac{\mathrm{d}^{2} \theta}{\mathrm{d} x^{2}} \delta x\right] \end{aligned}

So the net amount of heat gained per second by the element of thickness $δx$ , sandwitched between the two planes will be

eqn (3)

\begin{aligned} \mathrm{Q} & =\mathrm{Q}_{1}-\mathrm{Q}_{2}=-\mathrm{KA} \frac{\mathrm{d} \theta}{\mathrm{d} x}-\left[-\mathrm{KA}\left(\frac{\mathrm{d} \theta}{\mathrm{d} x}+\frac{\mathrm{d}^{2} \theta}{\mathrm{d} x^{2}} \delta x\right)\right] \\ & =\mathrm{KA} \frac{\mathrm{d}^{2} \theta}{\mathrm{d} x^{2}} \delta x \end{aligned}

This amount of heat is used to increase the temperature of the rod and a part of it lost due to radiation. Now, the following situations are possible.

Before the steady state is reached

The quantity of heat Q is used in two ways before the steady state is reached. Partly the heat is used to raise the temperature of the road and the rest is lost due to radiation.

Let the rate of rise of temperature of the bar be $dθ/dt$ . The heat used per second to raise the temperature of the rod $=$ mass x specific heat $\times$ (increase in temperature/time).

eqn (4)