Statement
Newton’s law of cooling states that the rate of cooling of a body is directly proportional to the temperature difference between the body and the surroundings.
The law holds good only for a small difference of temperature. Loss of heat by radiation depends on the nature of the surface and the area of the exposed surface.
If θ be the temperature at the instant of the cooling body and θ0 be the temperature of surroundings, the rate of loss of heat of the body
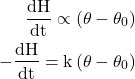\begin{aligned} \frac{\mathrm{dH}}{\mathrm{dt}} \propto\left(\theta-\theta_{0}\right) \\ -\frac{\mathrm{dH}}{\mathrm{dt}}=\mathrm{k}\left(\theta-\theta_{0}\right) \end{aligned} eqn (1)Negative sign indicates that the heat is lost. The proportionality constant depends upon the shape, area and nature of the exposed surface.
Derivation
Consider a body of mass m, specific heat C and at temperature θ. Let θ0 be the temperature of the surroundings. Suppose, that temperature falls by a small amount dθ in time dt. Then the amount of heat lost.
dH = mCdθ
∴ Rate of loss of heat
eqn (2)
\frac{\mathrm{dH}}{\mathrm{dt}}=\mathrm{mC} \frac{\mathrm{d} \theta}{\mathrm{dt}}From Newton’s law of cooling, the rate of heat is proportional to the difference of temperature (θ-θ0)
eqn (3)
-\frac{\mathrm{dH}}{\mathrm{dt}}=\mathrm{k}\left(\theta-\theta_{0}\right)Where K is a constant depending upon the area and the nature of the surface of the body.
From eqn. (2) and (3)
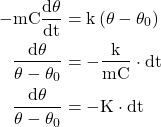\begin{aligned} -\mathrm{mC} \frac{\mathrm{d} \theta}{\mathrm{dt}} & =\mathrm{k}\left(\theta-\theta_{0}\right) \\ \frac{\mathrm{d} \theta}{\theta-\theta_{0}} & =-\frac{\mathrm{k}}{\mathrm{mC}} \cdot \mathrm{dt} \\ \frac{\mathrm{d} \theta}{\theta-\theta_{0}} & =-\mathrm{K} \cdot \mathrm{dt} \end{aligned} eqn (4)K=(k/mC) being another constant and is independent of t. Integrating both sides of eqn.(4)
\begin{aligned} \int \frac{d \theta}{\theta-\theta_{0}} & =\int-\mathrm{K} \cdot \mathrm{dt} \\ \log _{\mathrm{e}}\left(\theta-\theta_{0}\right) & =-\mathrm{Kt}+\mathrm{c} \end{aligned}Here, C is integration constant. A graph between loge (θ−θ0)and t must be a straight line.
| Read More Topics |
| Expression for bending moment of a beam |
| Crystal physics – solved problems |
| Poisson’s Ratio(σ) |
