Principle
Thermal conductivity of rubber can be determined by radial heat flow method and the quantity of heat flowing per second is determined by using a constant flow calorimeter.
Construction and working
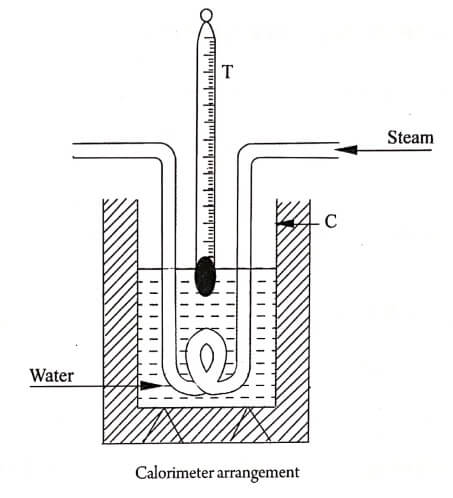
An empty calorimeter is taken and weighted. Let this be m1. Three fourths of the calorimeter is filled with water and weighted. Let this be m2. A rubber tube whose inner and outer radii are r1 and r2 is taken. A known length of the tube is immersed in the water in the calorimeter as shown in (Fig). Let the length be l. The initial temperature of water is noted. Let this be θ3. Steam from a steam chamber is allowed to pass through one end of the tube for a known time. Let the time be ‘t’ seconds. The water in the calorimeter should be stirred well, when the steam passes through the tube.
The final temperature is noted. Let this be θ4. If θ3 and θ4 are the initial and final temperature respectively, the average temperature of water and calorimeter is given by
eqn (1)
The temperature θ2 may be taken as the temperature of the outer side of the rubber tube in contact with the water. So if θ1 is the temperature of the steam passing through the tube, then the difference in temperature between inner and outer side of the tube is ![]()
| Rise in temperature = θ4 – θ3 |
| Heat gained by the calorimeter = m1s1 (θ4 – θ3 ) |
| Heat gained by water =(m2 -m1 ) s2 (θ4-θ3) |
Where s1 and s2 are specific heats of calorimeter and water respectively.
Total heat gained by calorimeter and water
=[m1s1 + (m2 – m1)s2](θ4-θ3)
Quantity of heat flowing per second
eqn (2)
![]()
But we know from cylindrical flow of heat
eqn (3)
![]()
Substituting the values of θ2 and Q in equation (3) we have
eqn (4)
![]()
Thermal conductivity of rubber can be calculated using eq (4).
| Read More Topics |
| Newton’s law of cooling |
| Expression for bending moment of a beam |
| Crystal physics – solved problems |