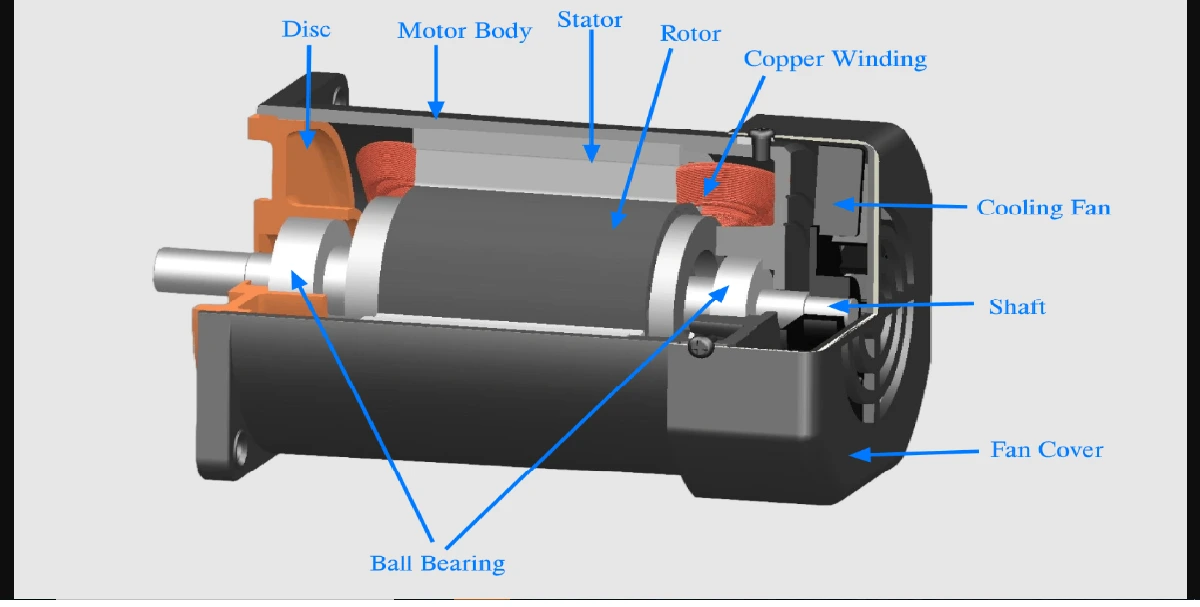
Zeroth law of thermodynamics states, “When two bodies are in thermal equilibrium with a third body separately, they are also in thermal equilibrium with each other”.
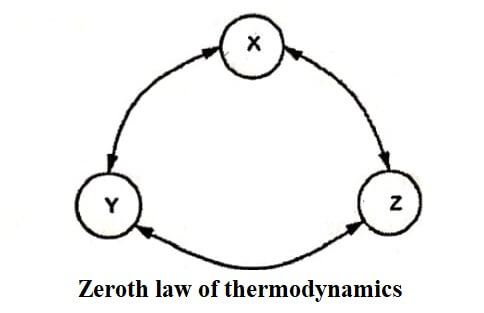
As shown in figure let, a system X be in thermal equilibrium with another system Y. Also, let, another system Z be in thermal equilibrium with the system Y. Then from Zeroth law of thermodynamics, the system X is in thermal equilibrium with the system Z. Hence, X and Z are at same temperatures.
Energy
Energy is a fundamental concept of thermodynamics and one of the most significant aspects of engineering analysis. Energy is defined as the capacity of a system to perform work or produce heat.
Energy can exist in numerous forms such as chemical, thermal, mechanical, magnetic, kinetic, potential, electric, and nuclear. Their sum constitutes the total energy (E) of a system.
In a thermodynamic analysis, various forms of energy which structure the total energy of a system are grouped into:
- Macroscopic forms of energies
- Microscopic forms of energies
The macroscopic forms of energy are those a system possesses as a whole with respect to some outside reference frame such as kinetic and potential energies. The macroscopic energy of a system is related to motion and the influence of some external effects such as gravity, magnetism, electricity, and surface tension.
The energy that a system possesses as a result of its motion relative to some reference frame is called kinetic energy (K.E). The kinetic energy is expressed by
\text { K.E. }=\frac{1}{2} m C^{2}Where, m be the mass of the system
C be the velocity of the system
The energy that a system possesses as a result of its elevation in a gravitational field is called potential energy (P.E). It is expressed by P.E = m g z
Where, g be the acceleration due to gravity
z be the elevation of the center of gravity of a system relative to some arbitrarily selected reference level the velocity of the system
The microscopic forms of energy are those related to the molecular structure of a system and the degree of the molecular activity and they are independent of outside reference frames.
The sum of all microscopic forms of energy is called internal energy (I.E) of a system and it is denoted by the letter U. Internal energy is related to the molecular structure and degree of molecular activity and it can be viewed as the sum of the kinetic and potential energies of the molecules. The kinetic include translational translational energy, vibrational kinetic kinetic energy, and spin energy.
The portion of the internal energy of a system associated with the kinetic energies of molecules is called sensible energy. The internal energy is also associated with various binding force between molecules of a substance. The internal energy associated with the phase of a system is called latent energy. The internal energy associated with atomic bonds in a molecule is called chemical energy. The tremendous amount of energy associated with the strong bonds within the nucleus of the atom itself is called nuclear energy.
None of these forms of energy can be measured or evaluated directly but techniques have been developed to evaluate the change in the total of all these microscopic forms of energy. These microscopic forms of energy are collectively called internal energy.
The magnetic, electric, and surface tension effects are only significant in some specialized cases and they are usually ignored. Therefore, the total energy of a system consists of kinetic, potential, and internal energies and is expressed by
\begin{aligned} \mathrm{E} &=\mathrm{K} . \mathrm{E} .+\mathrm{P.E} .+\mathrm{I} \mathrm{E} \\ &=\frac{1}{2} m C^{2}+m g z+U \end{aligned}| Read More Topics |
| Basic communication system |
| Electrical thermal resistance |
| Gas turbine power plant |
