NEED FOR CHANNEL CODING
The presence of noise in a channel generally, causes discrepancies between the output and input data sequences of a digital communication system.
For example, in wireless communication channel, the error probability may be 10-1, which means that only 9 out of 10 transmitted bits are received correctly. But, in many applications this level of reliability is unacceptable.
A probability of error equal to 10-6 (or) even lower is often a necessary requirement. In. order to achieve that requirement we have to use a Channel Coding.
The goal is to increase the resistance of a digital communication system to channel noise.
Channel Coding Progress
Channel coding consists of mapping the incoming data sequence into a channel input sequence using encoder at the transmitter and the decoder at the receiver inverse mapping the output sequence into an output data sequence in such a way that the overall effect of channel noise on the system is minimized.
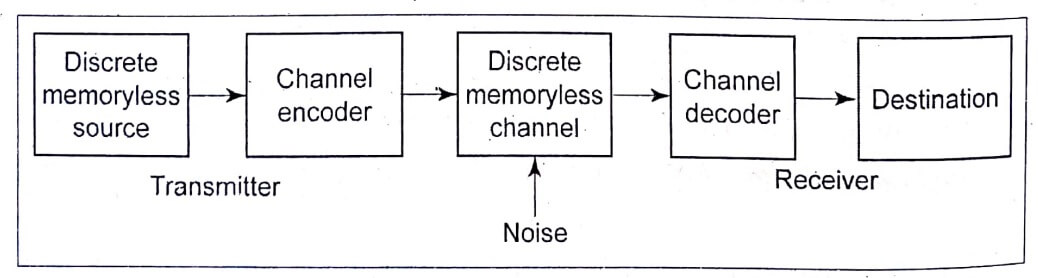
Fig.1. Block Diagram of Digital Communication System
In the channel encoding process, introduce redundancy in the channel encoder so as to reconstruct the original source sequence as accurately as possible.
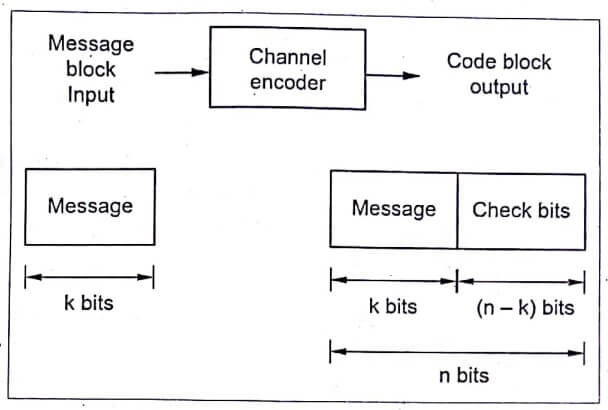
Consider block codes, in which the message sequence is divided into sequential blocks of k bits. Then, the k bits is mapped into n-bit block, such that, the number of redundant bits added is 𝑛−𝑘 bits ( 𝑛>𝑘 ).
Code rate (or) code efficiency =\frac{\text { No of message bits in a block }}{\text { No of bits in code word }} eqn (1)
\text { Code rate, } r=\frac{k}{n} \text {, always }<1Channel coding is efficient when the code rate is high, which can be defined using channel capacity. Accurate reconstruction of the original source sequence at the destination requires average probability of symbol error should be less.
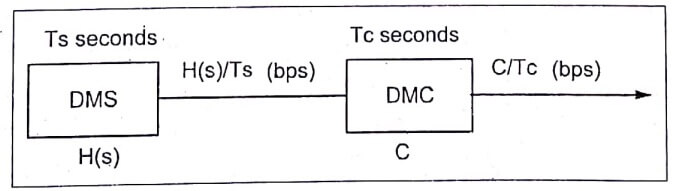
Fig.3. DMS & DMC model
DISCRETE MEMORYLESS SOURCE (DMS)
- Consider a Discrete Memoryless Source (DMS) with an alphabet S and Entropy 𝐻(𝑆) bits per source symbol and source emits symbols once every 𝑇s seconds.
eqn (2)
Average information rate of the source = H(S)/Ts bits/sec
- The decoder delivers decoded symbols to the destination from the source alphabet S and the same source rate of symbol every Ts.
DISCRETE MEMORYLESS CHANNEL (DMC)
- The Discrete Memoryless Channel (DMC) has a channel capacity equal to C bits per use of the channel and used once every Tc seconds.
eqn (3)
Channel Capacity per units = C/TC bits/sec
- This represents the maximum rate of information transfer over the channel.
STATEMENT
The channel coding theorem for a discrete memory less channel is stated in two parts as follows:
(i) Let DMS with an alphabet S have entropy H(S) and produce symbols at every Ts seconds. Let DMC have capacity C and used once every Tc seconds. Then if,
eqn (4)
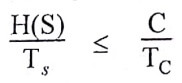
There exists a coding scheme for which source output can be transmitted over the channel and can be reconstructed with the small probability of error.
eqn (5)
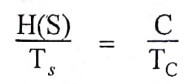
Then, the system is said to be signaling at the critical rate.
eqn (6)
(ii) if,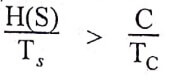 
No possibility of transmission and reconstruction of information with small probability of error.
The channel coding theorem states that the channel capacity C as a fundamental limit on the rate at which the transmission of reliable error-free messages can take place over a discrete memoryless channel. It is important to note the following points,
- It doesn’t show us how to construct a good code.
- It doesn’t have a precise result for the probability of symbol error after decoding the channel output.
- Power and Bandwidth constraints also hidden here.
| Read More Topics |
| Electrochemistry – Questions and Answers |
| Energy sources – Questions and Answers |
| Introduction of error control codes |
