In the following sections, the frequency of transverse vibrations of various systems and the phenomenon of whirling speed have been discussed.
Natural Frequency of Free Transverse Vibrations
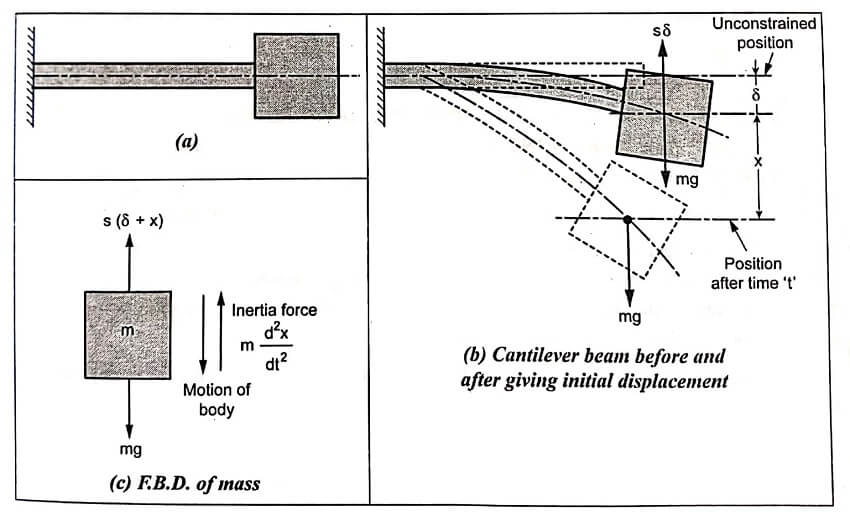
Consider a shaft of negligible mass, whose one end is fixed and the other end carries a body of weight W, as shown in Fig (a). Fig (b) shows all three positions: (i) unconstrained position, (ii) mean or equilibrium position, and (iii) position after time ‘t’. The various forces acting on the mass are shown in Fig (c).
Now this problem is very much similar to that of longitudinal vibrations discussed in next section. Thus the relation derived in next section for natural frequency of longitudinal vibrations holds good for transverse vibrations also.
\therefore \text { Circular frequency, } \omega_{n}=\sqrt{\frac{s}{m}}Time period of the transverse vibrations, t_{p}=2 \pi \sqrt{\frac{m}{s}} and the natural frequency of the transverse vibrations,
f_{n}=\frac{1}{t_{p}}=\frac{1}{2 \pi} \sqrt{\frac{s}{m}}=\frac{1}{2 \pi} \sqrt{\frac{g}{\delta}}=\frac{0.4985}{\sqrt{\delta}}Effect of Inertia of the Constraint in Transverse Vibrations
When the mass of the constraint ‘mc‘ and the mass of the disc ‘m’ of a transverse vibrations are given, then the effect of inertia of the constraints are:
- If the constraint is like a cantilever beam, then 33/140 of its mass may be added to the mass of the disc while calculating the natural frequency of transverse vibrations.
- If the constraint is like a simply supported beam, then 17/35 of its mass may be added to the mass of the disc.
- If both the ends of the constraint are fixed, then 13/35 of its mass may be added to the mass of the disc.
