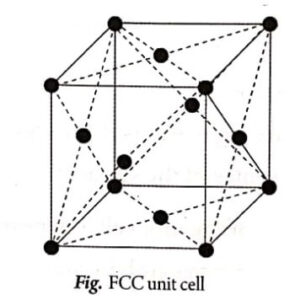
A face centred cubic structure consists of eight corner atoms and six face centred atoms.
Examples: Copper, Nickel, Gold, Lead and Platinum.
The arrangement of atoms in face centred cubic unit cell is shown in Fig.
Number of atoms per unit cell
An FCC unit cell consists of eight corner atoms and each and every corner atoms is shared by eight adjacent unit cells. Therefore, each and every corner atom contributes \frac{1}{8} of its part to one unit cell.
∴ The total number of atoms by corner atom \frac{1}{8} \times 8=1 atom.
In addition, there are 6 atoms at the face centeres of the cube. Each face centred atoms is shared by two surrounded unit cells. Hence, the number of face centred atoms in unit cell,
=\frac{1}{2} \times 6=3 \text { atoms. }∴ Total number of atoms in one unit cell = 1 + 3 = 4 atoms.
Co-ordination number
In this case, there are eight atoms at the eight corners of the unit cell and 6 atoms at the centre of the six faces.
For any corner atom of the unit cell, the nearest atom is the face centred atom. For any corner atom, there are four face centred atoms in its plane and four above its plane and four below its plane.
Thus, the co-ordination number of this case = 4+4+4 = 12.
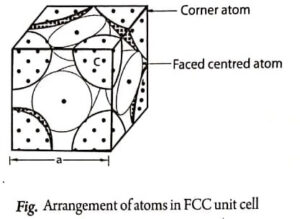
Atomic radius
For an FCC unit cell, the atomic radius can be calculated from Fig. as follows:
\begin{aligned} & D B^2=D C^2+C B^2 \\ & (4 r)^2=a^2+a^2 . \\ & 16 r^2=2 a^2 \\ & r^2=\frac{2 a^2}{16} \\ & r=\frac{\sqrt{2 a^2}}{\sqrt{16}} \end{aligned}
Atomic radius r=\frac{a \sqrt{2}}{4}
Atomic packing factor
Number of atoms per unit cell = 4
Volume of 4 atoms \text { (v) }=4 \times \frac{4}{3} \pi r^3
Radius of atom in FCC \quad(r)=\frac{a \sqrt{2}}{4}
Volume of the unit cell (V) = a³
Volume occupied by the total
\text { Atomic packing factor }=\frac{\text { number of atoms per unit cell }(v)}{\text { Total volume of the unit cell }(V)} \begin{aligned} = & \frac{4 \times \frac{4}{3} \pi r^3}{\left(\frac{4 r} \sqrt{2}}\right)^3}=\frac{\frac{16}{3} \pi r^3}{\frac{4^3 r^3} (\sqrt{2})^3}}=\frac{\frac{16}{3} \pi r^3}{\frac{64 r^3}{2 \sqrt{2}}} \\ = & \frac{16}{3} \times \frac{2 \sqrt{2}}{64} \pi=\frac{\pi \sqrt{2}}{6} \\ A P F= & 0.74 \end{aligned}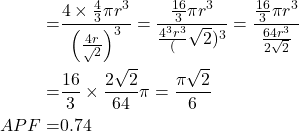Therefore, 74% of the volume is occupied by the atoms and remaining 26% of the volume is vacant in FCC structure.
Thus, the packing density is 74%. Since the packing density is high the FCC structure has tightly packed structure.
| Read More Topics |
| Important parameters in crystal structure |
| Classification of solids crystal physics |
| Classification of nonlinear materials |
