Bodies in series
Let us consider a compound media like a slab or a wall made up of two different materials A and B having thickness x1 and x2 as shown in (Fig. 1)
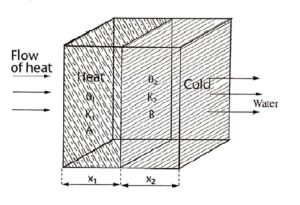
Fig. (1) Bodies in series
Let the temperature of two end faces be θ1 and θ2.
Let the temperature of the common surface be θ.
Let K1 and K2 be the thermal conductivities of A and B respectively.
If we consider θ1>θ2, so that heat flow will be from A to B and when the steady state is reached
eqn (1)
\theta=\frac{\mathrm{K}_{1} \mathrm{~A}\left(\theta_{1}-\theta\right)}{x_{1}}
eqn (2)
and for B medium, 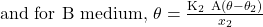\text { and for B medium, } \theta=\frac{\mathrm{K}_{2} \mathrm{~A}\left(\theta-\theta_{2}\right)}{x_{2}}
Now at steady state,
we have, \frac{\mathrm{K}_{1} \mathrm{~A}\left(\theta_{1}-\theta\right)}{x_{1}}=\frac{\mathrm{K}_{2} \mathrm{~A}\left(\theta-\theta_{2}\right)}{x_{2}}
(i.e.)
\frac{\mathrm{K}_{1} \theta_{1}}{x_{1}}-\frac{\mathrm{K}_{1} \theta}{x_{1}}=\frac{\mathrm{K}_{2} \theta}{x_{2}}-\frac{\mathrm{K}_{2} \theta_{2}}{x_{2}}
(i.e.) \left(\frac{\mathrm{K}_{1}}{x_{1}}+\frac{\mathrm{K}_{2}}{x_{2}}\right) \theta=\left(\frac{\mathrm{K}_{1} \theta_{1}}{x_{1}}+\frac{\mathrm{K}_{2} \theta_{2}}{x_{2}}\right)
(i.e.) \theta=\frac{\frac{\mathrm{K}_{1} \theta_{1}}{x_{1}}+\frac{\mathrm{K}_{2} \theta_{2}}{x_{2}}}{\frac{\mathrm{K}_{1}}{x_{1}}+\frac{\mathrm{K}_{2}}{x_{2}}}
eqn (3)
(i.e.) \theta=\frac{\sum \frac{\mathrm{K}_{1} \theta_{1}}{x_{1}}}{\sum \frac{\mathrm{K}_{1}}{x_{1}}}
Putting the value of θ in eqn (1) or (2) we can get the quantity of heat flowing through the compound media.
| Read More Topics |
| De-Broglie’s concept of matter |
| Laws for explaining the energy distribution |
| Characteristics of De-Broglie waves |
