When a dielectric material is placed in an external electric field, it exerts a dipole moment in it.
The total electric field at the atom site of the dielectric kept in an applied electric field is called the internal field. It is given by the sum of the applied field (E) and the electric fields created by the neighbouring atoms (E’).
Ei = E + E’
Lorentz method to find the internal field
Let a dielectric material is placed in between two charged places of a parallel plate capacitor as shown in fig below.
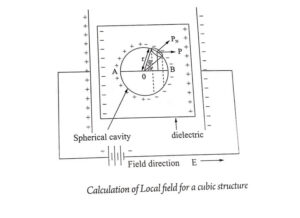
Assume an imaginary small spherical cavity around an atom for which the internal field must be calculated at its centre.
The internal field Eint at the atom site (O) can be considered to consist of components namely E1, E2, E3 and E4.
eqn. 1
Eint = E1 + E2 + E3 + E4
E1 – Field intensity at O die to the charge density on the plates.
E2 – Electric field due to the polarized charges (induced charges) on the plane surface of the dielectric.
E3 – Electric field due to polarised charges induced on the surface of the imaginary spherical cavity.
E4 – Electric field due to permanent dipoles of the atoms inside the spherical cavity considered.
Macroscopically, we can take E = E1 + E2 the field externally applied (E1) and the field induced on the plane surface of the dielectric (E2) can be considered as a single field (E).
If we consider the dielectric which is highly symmetric, then the field due to the dipoles present inside the imaginary cavity will cancel each other. Therefore, the electrical field due to permanent dipoles E4 = 0.
The eqn. (1) can be written as
eqn. 2
Eint = E + E3
Determination of E3
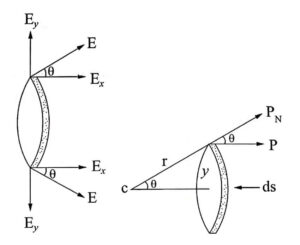
Let us consider a small area ‘ds’ on the surface of the spherical cavity. The small area makes an angle dθ at the center at an angle θ with the direction of the field E.
The polarization P will be parallel to E. PN is the component of polarization perpendicular to the area ds, and q’ is the charge on the area ds.
Polarisation is also defined as the surface charges per unit area.
\text { Hence, } \mathrm{P}_{\mathrm{N}}=\mathrm{P} \cos \theta=\frac{\mathrm{q}^{\prime}}{\mathrm{ds}}Charge on ds, q’ = Pcos θ ds
Electric field intensity at ‘O’ due to charge q, E=\frac{q \text { ' }}{4 \pi \varepsilon_0 \mathrm{r}^2}
eqn. 3
\mathrm{E}=\frac{\mathrm{PCosds}}{4 \pi \varepsilon_0 \mathrm{r}^2}This field intesity is along the radius ’r’ and it can be resolved into two components as shown in Fig (a).
The component of intensity parallel to the field direction
\begin{aligned} \mathrm{E}_{\mathrm{x}} & =\mathrm{E} \cos \theta \\ \mathrm{E}_{\mathrm{x}} & =\frac{\mathrm{P} \cos \theta \mathrm{ds} \cos \theta}{4 \pi \varepsilon_0 \mathrm{r}^2} \quad\left[\begin{array}{l} \because \sin \theta=\frac{\mathrm{y}}{\mathrm{r}} \\ \mathrm{y}=\mathrm{r} \sin \theta \end{array}\right] \\ \text { i.e., } \quad \mathrm{E}_{\mathrm{x}} & =\frac{\mathrm{P} \cos ^2 \theta \mathrm{ds}}{4 \pi \varepsilon_0 \mathrm{r}^2} \end{aligned} eqn. 4The component of intensity perpendicular to the field direction
Ey = E sin θ
Since the perpendicular components are in opposite direction Fig. (a), they cancel out each other. So the parallel components alone are taken into consideration.
Consider a ring area ds which is obtained by revolving ds about AB. Fig (b).
Ring area ad = Circumference × thickness
= 2πy × rdθ
eqn. 5
ds = 2πr2 sinθ dθ
Electric field intensity due to the elemental ring =\frac{P \cos ^2 \theta \mathrm{ds}}{4 \pi \varepsilon_0 \mathrm{r}^2} eqn. 6
Substituting eqn. (5) in eqn. (6)
\begin{aligned} & =\frac{P \cos ^2 \theta}{4 \pi \varepsilon_0 r^2} \times 2 \pi r^2 \sin \theta \cdot d \theta \\ & =\frac{P \cos ^2 \theta \sin \theta d \theta}{2 \varepsilon_0} \end{aligned} eqn. 7
Electric field intensity due to charge present in the whole sphere is obtained by integrating eqn. (7) within the limits 0 to π. This field is taken as E3.
\begin{aligned} & \mathrm{E}_3=\int_0^\pi \frac{P \cos ^2 \theta \sin \theta \mathrm{d} \theta}{2 \varepsilon_0} \\ & \mathrm{E}_3=\frac{\mathrm{P}}{2 \varepsilon_0} \int_0^\pi \cos ^2 \theta \sin \theta \mathrm{d} \theta \\ & \mathrm{E}_3=\frac{\mathrm{P}}{2 \varepsilon_0} \times \frac{2}{3} \quad\left[\because \int_0^\pi \cos ^2 \theta \sin \theta \mathrm{d} \theta=\frac{2}{3}^{-}\right. \\ & \mathrm{E}_3=\frac{\mathrm{P}}{3 \varepsilon_0} \end{aligned} eqn. 8Substituting eqn. (8) in eqn. (2) , we get
eqn. 9
\mathrm{E}_{\text {int }}=\mathrm{E}+\frac{\mathrm{P}}{3 \varepsilon_0}where Eint is called internal field or Lorentz field.
This eqn. (9) shows that Eint is different from E. The local intensity Eint is larger than the macroscopic intensity E. So the molecules are more effectively polarised.
| Read More Topics |
| Frequency and temperature dependance of polarization |
| Polar and non-polar molecules |
| Applications of superconducting materials |
