The amount of light rays which is accepted by the fibre is known as numerical aperture (NA).
Let n1 and n2 be the refractive indices of core and cladding and let be the refractive index of the medium (air) in which the optical fibre is placed.
Now applying the Snell’s law of refraction at the point of entry of the ray AO into the core, we have,
eqn (1)
N0 sin θa = n1 sin θr
At the point B on the interface of the core and cladding, angle of incidence
Applying Snell’s law of refraction again,
eqn (2)
![Rendered by QuickLaTeX.com \begin{array}{rlr} \mathrm{n}_1 \sin \left(90-\theta_{\mathrm{r}}\right) & =\mathrm{n}_2 \sin 90^{\circ} & \\ \mathrm{n}_1 \cos \theta_{\mathrm{r}} & =\mathrm{n}_2 & {\left[\sin 90^{\circ}=1\right]} \\ \cos \theta_{\mathrm{r}} & =\frac{\mathrm{n}_2}{\mathrm{n}_1} \end{array}](https://pedagogyzone.com/wp-content/ql-cache/quicklatex.com-d00a358dfc3e74b2760989d746286ab2_l3.png)
Rewriting equation (1), we have
eqn (3)
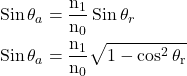
eqn. (2) sub in eqn. (3)
eqn (4)
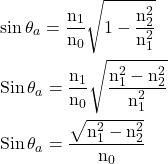
eqn (5)
∴Acceptance angle ![]()
If the refractive index of air (n0)=1
eqn (6)
∴ Acceptance angle ![]()
Thus, the maximum angle of incidence for which the light ray is totally reflected at the core-cladding interface and propagates through the fibre is called the acceptance angle.
The sin of the acceptance angle of the fibre is known as numerical aperture (NA). It denotes the light collecting efficiency of the fibre and is the measure of the amount of the light rays that can be accepted by the fibre.
eqn (7) & (8)
![Rendered by QuickLaTeX.com \begin{aligned} \therefore \quad N A & =\operatorname{Sin} \theta_a \\ \quad N A & =\operatorname{Sin}\left[\operatorname{Sin}^{-1} \sqrt{\mathrm{n}_1^2-\mathrm{n}_2^2}\right] \\ N A & =\sqrt{\mathrm{n}_1^2-\mathrm{n}_2^2} \end{aligned}](https://pedagogyzone.com/wp-content/ql-cache/quicklatex.com-85427f88f26c4e60d08f0a5dd6cd1328_l3.png)
Fractional index change (Δ)
It is the ratio of the refractive index difference in core and cladding to the refractive index of core.
eqn (1)
![]()
Relation between NA and Δ
we know that ![]()
(or)
eqn (2)
![]()
eqn (3)
From eqn. (1) ![]()
eqn. (3) sub in eqn. (2)
![]()
If n1≈ n2 then
![]()
eqn (4)
∴![]()
| Read More Topics |
| Introduction and construction of fibre optics |
| Principle and propagation of light in optical fibres |
| Industrial applications laser welding |