The macroscopic magnetic properties of a substance are a consequence of magnetic moments associated with individual electrons. The electrons in an atom revolved around the nucleus in different orbits.
Each electron in an atom has magnetic moments that originate from the following sources.
- The orbital magnetic moment of electrons (the motion of electrons in the closed orbits around the nucleus). It is called as orbital motion of electrons. Its magnitude is always small.
- Spin magnetic moment of the electrons (due to electron spin angular momentum) and it is called as spin motion of the electrons.
- Nuclear spin (due to nuclear spin angular momentum). Since, this is nearly 103 times smaller than that of electron spin, it is not taken into consideration.
Atom consists of central positively charged massive nucleus and electrons. The electrons revolve around the nucleus in different circular orbits. But, when an electron moves around a fixed point in a circular orbit, it produces magnetic field perpendicular to the plane of the orbit. So, if a charged particle has an angular momentum, it behaves as an elementary magnet. Thus, an atom possesses magnetic dipole moment and behaves as a magnetic dipole.
Magnetic moments associated with an orbiting electron and a spinning electron is shown in Fig.
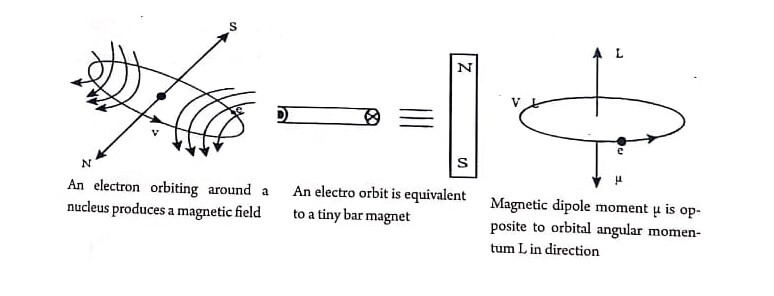
Orbital angular momentum of the electron
This corresponds to a permanent magnetic dipole moments.
Let us consider an e−describing a circular orbit of radius ‘r’ with a stationary nucleus at the centre as shown in Fig. Let the e– rotate with a constant angular velocity of ‘ ω’ radians per second.
Electrons revolving in any orbit may be considered as current carrying circular coil producing magnetic field perpendicular to its plane. Thus the electronic orbits are associated with a magnetic moment. The orbital magnetic moment of an e– in an atom can be expressed in terms of atomic unit of magnetic moment called Bohr Magneton. It is also defined as the unit of measurement of atomic magnetic moment.
1 Bhor Magnetron =\mu_B=\frac{\text { electron charg e } \times \text { Plancks constant }}{2 \times \text { Electron mass }}
\mu_{\mathrm{B}}=\frac{\mathrm{e} \hbar}{2 \mathrm{~m}_{\mathrm{e}}}=\frac{\mathrm{e}}{\mathrm{m}_{\mathrm{e}}} \frac{\mathrm{h}}{4 \pi}
Electron spin magnetic Moment
The concept of the e– having an angular momentum has been introduced in order to explain the details of atomic spectra. This angular momentum of the e– is referred to as the spin of the e–. Since the e– has a charge, its spin produces a magnetic dipole moment. According to quantum theory, the spin angular momentum along a given direction is either
\frac{+\mathrm{h}}{4 \pi} \text { (or) } \frac{-\mathrm{h}}{4 \pi}Hence, the spin dipole moment components along an external field are
\begin{aligned} & \frac{\mathrm{e}}{\mathrm{m}} \cdot \frac{\mathrm{h}}{4 \pi}=+1 \text { Bohr magneton (or) } \\ & -\frac{\mathrm{e}}{\mathrm{m}} \cdot \frac{\mathrm{h}}{4 \pi}=-1 \text { Bohr magneton } \end{aligned}In a many electron atom, the individual spin magnetic moments are added in accordance with certain rules. Completely filled shells contribute nothing to the resultant spin moment.
Nuclear Magnetic Moment
The angular momentum associated with the nuclear spin is also measured in units of ℎ/2π. The mass of the nucleus is larger than that of an e– by the order of 103. Hence, nuclear spin magnetic moment is of the order of 10-3 Bohr magnetrons.
| Read More Topics |
| Difference between intrinsic & extrinsic semiconductors |
| Variation of carrier concentration with temperature |
| Difference between N & P type semiconductor |
