When the dielectric material is placed in an electric field, the electric field realigns the dipoles resulting in polarization. Polarization occurs in a dielectric material when it is subjected to an external electric field.
There are four polarisation mechanisms.
They are
- Electronic polarization,
- Ionic polarization,
- Orientation polarisation and
- Space charge polarisation.
Electronic or Induced Polarisation
Electronic polarization occurs due to the displacement of positively charged nucleus and negatively charged electrons in opposite directions, when an external electric field is applied, and thereby creates a dipole moment in the dielectric.
∴ The induced dipole moment μ = αeE
where αe = electronic polarizability
Monoatomic gases exhibit this kind of polarization. Electronic polarizability is proportional to the volume of the atoms and is independent of temperature.
Calculation of electronic polarizability
(i) Without field
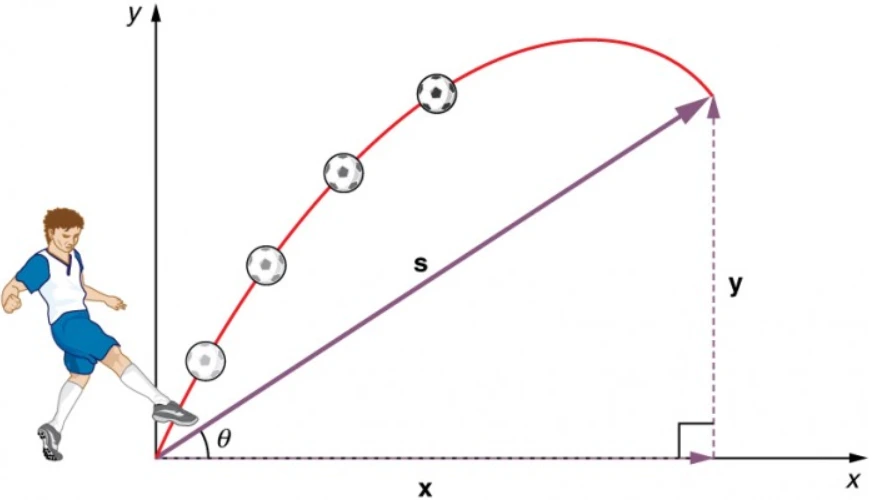
Let us consider a classical model of an atom. Assume the charge of nucleus of that atom is Ze. The nucleus is surrounded by an electron cloud of charge −Ze, which is distributed in a sphere of radius R as shown in Fig (a).
The charge density of the sphere is given by ![]()
![]()
eqn. 1
(or) charge density ![]()
(ii) With field
When the dielectric is placed in a d.c. electric field (E), two phenomenon occur.
- Lorentz force due to the electric field tends to separate the nucleus and the electron cloud from their equilibrium position.
- After separation, an attractive Coulomb force arises between the nucleus and electron cloud which tries to maintain the original equilibrium position.
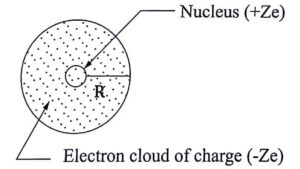
Let x be the displacement made by the electron cloud from the positive core, as shown in Fig (b). Since the core is heavy, it will not move when compared to the movement of electron cloud. Here x<<R, where R is radius of the atom.
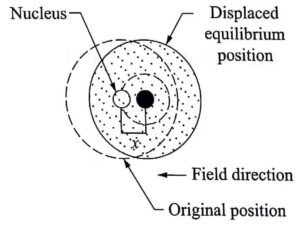
Since Lorentz and Coulomb forces are equal and opposite in nature, equilibrium is reached.
At equilibrium
eqn. 2
Lorentz force = Coulomb force
Lorentz force = Charge × Filed
Lorentz force = -ZeE
The negative sign indicates the repulsive force.
Coulomb force = Charger × Field
![]()
eqn. 3
Coulomb force ![]()
The positive sign indicates the attractive force
Here, Total number of negative charges (Q) enclosed in the sphere of radius x = Charge density of electrons × Volume of the sphere
Substituting the charge density from eqn. (1), we get
Total number of negative charges (Q) enclosed in the radius x
![]()
eqn. 4
![]()
Substituting eqn. (4) in (3) we get eqn. 5
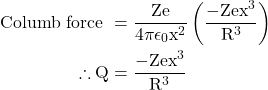
At the equilibrium position, Lorentz force = Coulomb force
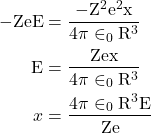 eqn. 6
eqn. 6
Therefore, the displacement of electron cloud (x) is proportional to applied electric field E.
Dipole moment
Now the two electric charges +Ze and −Ze are displaced by a distance ‘x’ under the influence of the field and form an induced dipole moment which is given by
Induced dipole moment (μe) = Magnitude of charge x displacement
=Zex
Substituting the value of x from equation (6), we have
![]()
μe = 4π ∈0 R3E
μe α E
μe = αeE
where μe = 4π ∈0 R3E (Farad-m2) is called electronic polarization which is proportional to volume of the atom.
Ionic or Induced Polarisation
Ionic polarization is due to the displacement of cations (positive ions) and anions (negative ions) in opposite directions and occurs only in those dielectric materials which possess ionic bond. In this ionic crystal, there is a transfer of electron from one atom to another.
Example : NaCl crystal, KBr, KCl, etc.,
For an example, in the sodium chloride crystal (NaCl). there is a transfer of an electron Na+ atom to Cl– atom.
Explanation
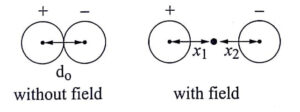
A sodium chloride molecule has one cation and one anion present in each unit cell of the ionic crystal and their interatomic distance is ‘d’.
Such molecule have built in permanent dipole moment equal to do which exists even before the field is applied. Such materials are said to be polar. When the electric field is applied, let x1, x2 be the distances to which positive and negative ions move from their equilibrium positions. The resultant dipole moment per unit cell, due to ionic displacement is given by
Induced dipole moment = magnitude of charge x displacement
eqn. 1
∴ μi = e (x1 + x2)
where
x1 is the shift of positive ion.
x2 is the shift of negative ion
When the field is applied the restoring force produced is proportional to the displacements
For +ve ions
Restoring force
F α x1
eqn. 2
F = β1 x1
For -ve ions
Restoring force
F α x2
eqn. 3
F = β2 x2
β1 β2 is the restoring force constants. It depends on the mass of ions and angular frequency of the molecule in which ions are present.
If ‘m’ is the mass of +ive ion and ‘M’ is the mass of negative ion an ω0 is the angular frequency then
eqn. 4
β1 = mω02.
eqn. 5
β2 = Mω02
Substituting β1 in eqn. (2) the restoring force for positive ion can be written as
eqn. 6
F = m ω02 x1
eqn. 7
We know F = eW
Equating eqn. (6) and (7) we get
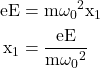 eqn. 8
eqn. 8
Substituting β2 in eqn. (3) the restoring for negative ion can be written as
eqn. 9
F = Mω02 x2
eqn. 10
We know F = eE
Equating eqn. (9) and (10) we get
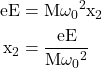 eqn. (11)
eqn. (11)
Adding eqn. (8) and (11) we get
eqn. 12
![]()
Substituting eqn. (12) in (1) we get
![]()
Or
μi = αiE
where αi is called the ionic polarizability and it is given by
![]()
So the ionic polarizability is inversely proportional to the square of natural frequency of the ionic molecule and directly proportional to its reduced mass given by ![]()
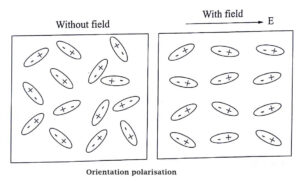
Orientational or Dipolar Polarisation
The orientational polarization is observed only for polar dielectrics. The molecules of polar dielectric materials have permanent dipole moment even in the absence of an electric field.
Example : CH3Cl, H2O, HCl, etc.,
In absence of any external electric field, the permanent dipole moment are randomly oriented so that they cancel the effects of each other. Hence, the net dipole moment of the material is zero.
But, when the electric field is applied to a polar molecules, the dipoles experience a torque and try to get aligned themselves in the direction of applied field. A net dipole moment thus develops.
The polarisation that appears due to the alignment of permanent dipoles in a material in the direction of applied electric field on it, is called orientational polarization.
From Langevin’s theory of paramagnetism
eqn. 1
![]()
The same principle can be applied to the application of electric field in dielectric
eqn. 2
![]()
where N is the number of atoms
Orientation polarization is inversely proportional to the temperature and proportional to the square of permanent dipole moment.
eqn. 3
![]()
Comparing (2) and (3) we get
![]()
Where α0 is orientational polarisability.
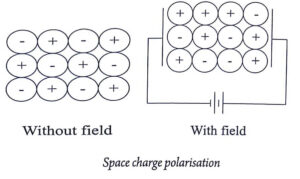
Space Charge Polarization
The polarization that appears due to the displacement of positive charges and negative charges of a multiphase dielectric material at its opposite interfaces due to the application of electric field on it, is called space charge polarisation.
The space charge polarization mechanism strongly depends on temperature.
In absence of an electric field, there is no seperation between the positive charges and negative charges within the material.
But, when the electric field specially at high temperature, the positive charges and negative charges are accumulated at the opposite interfaces of the material.
Total Polarization
The total polarization is equal to the sum of electronic, ionic, orientational and space charge polarization. When compared to other kind of polarization, space charge polarization is very small so it can be neglected.
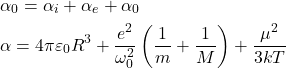
We know total polarization,
![Rendered by QuickLaTeX.com \begin{aligned} & \mathrm{P}=\mathrm{NE} \alpha \\ & \mathrm{P}=\mathrm{NE}\left[4 \pi \varepsilon_{\mathrm{O}} \mathrm{R}^{3}+\frac{\mathrm{e}^{2}}{\omega_{\mathrm{O}}{ }^{2}}\left(\frac{1}{\mathrm{~m}}+\frac{1}{\mathrm{M}}\right)+\frac{\mu^{2}}{3 \mathrm{kT}}\right] \end{aligned}](https://pedagogyzone.com/wp-content/ql-cache/quicklatex.com-a9dccb4a361578c9c07d5446f6cc11ac_l3.png)
This equation is called as Langevin-Debye equation.
| Read More Topics |
| Polar and non polar molecules |
| Classification of dielectric materials |
| Applications of superconducting materials |