Amplitude Modulation

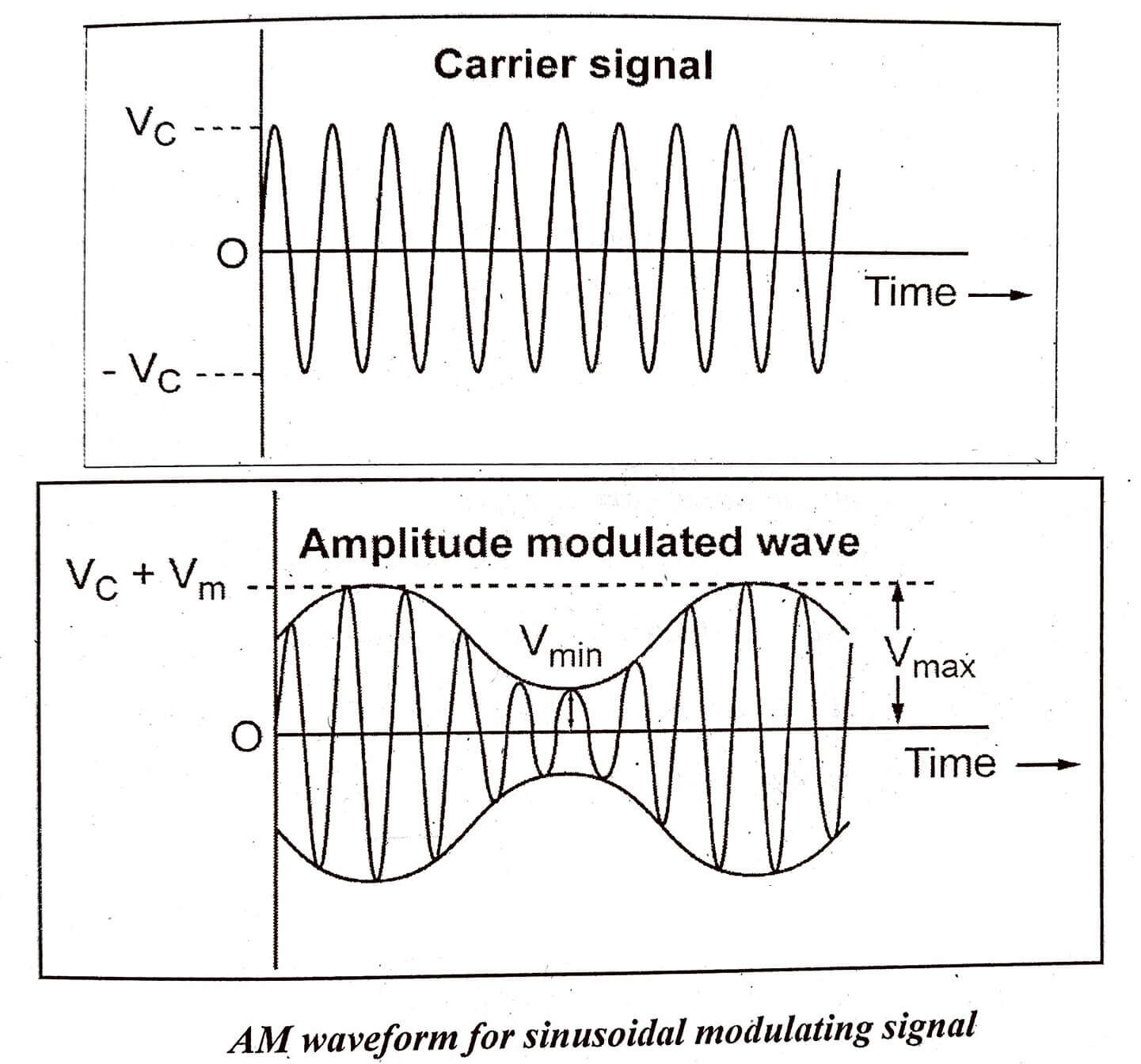
Mathematical or Time Domain Representation of an AM

Equ-1 Modulating signal \mathrm{V}_m(t)=\mathrm{V}_m \cos \omega_m t

Equ-2 Carrier signal \mathrm{V}_c(t)=\mathrm{V}_c \cos \omega_c t

Where,
\mathrm{V}_c – Amplitude of the carrier signal (volts), and
\mathrm{V}_m – Amplitude of the modulating signal (volts).
The amplitude of the carrier signal is changed after amplitude modilation, which is the amplitude of an AM wave and is expressed as,

Equ-3
\mathrm{V}_{\mathrm{AM}}=\mathrm{V}_c+\mathrm{V}_m(t)

By substitute equation (1) in equation (3), we get
\begin{aligned} & =\mathrm{V}_c+\mathrm{V}_m \cos \omega_m t \\ & =\mathrm{V}_c\left[1+\frac{\mathrm{V}_m}{\mathrm{~V}_c} \cos \omega_m t\right] \end{aligned}

Equ-4 \mathrm{V}_{\mathrm{AM}}=\mathrm{V}_c\left(1+m_a \cos \omega_m t\right) 

Modulation index of \mathrm{AM}=m_a=\frac{V_m}{V_C}

Hence, AM wave can be expressed as,

Equ-5 \mathrm{V}_{\mathrm{AM}}(t)=\mathrm{V}_{\mathrm{AM}} \cos \omega_c t 

By substituting equation (4) for the amplitude of an AM signal in equation (5), we get

Equ-6
\mathrm{V}_{\mathrm{AM}}(t)=\mathrm{V}_c\left(1+m_a \cos \omega_m t\right) \cos \omega_c t 

In terms of frequency, that is, \omega=2 \pi f , than the AM wave from equation (6) may be expressed as,

Equ-7
\mathrm{V}_{\mathrm{AM}}(t)=\mathrm{V}_c\left(1+m_a \cos 2 \pi f_m t\right) \cos \left(2 \pi f_c t\right) 

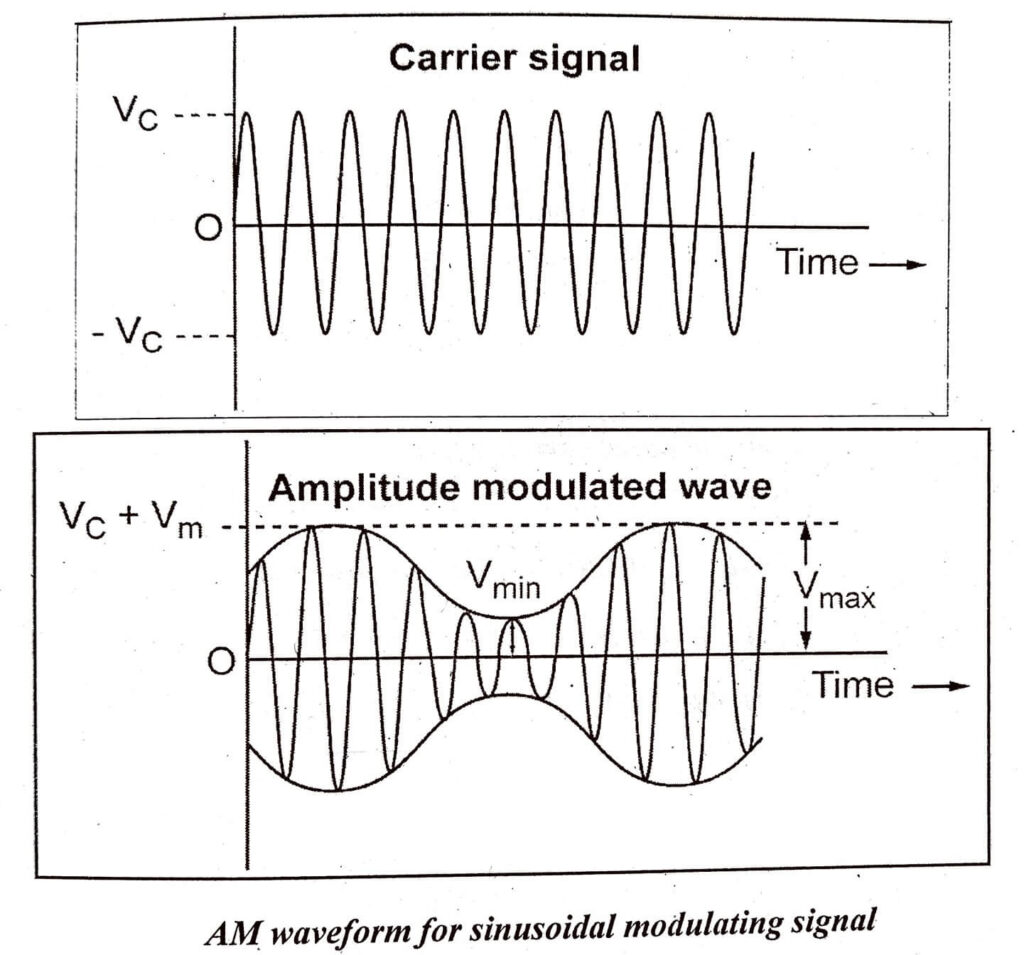
Equations (6) and (7) are called as time domain representations of an AM signal.

This Amplitude Modulation Double Sideband Full Carrier (AM DSB-FC) is sometimes called conventional \boldsymbol{A M} or simply \boldsymbol{A M} . The shape of the AM modulated wave is called as \boldsymbol{A M} envelope which contains all the frequencies and is used to transfer the information through the system.

An increase in the modulating signal amplitude causes the amplitude of the carrier to increase. The shape of the AM envelope is identical to the shape of the modulating signal.