Resistance and Conductance - Pedagogy Zone

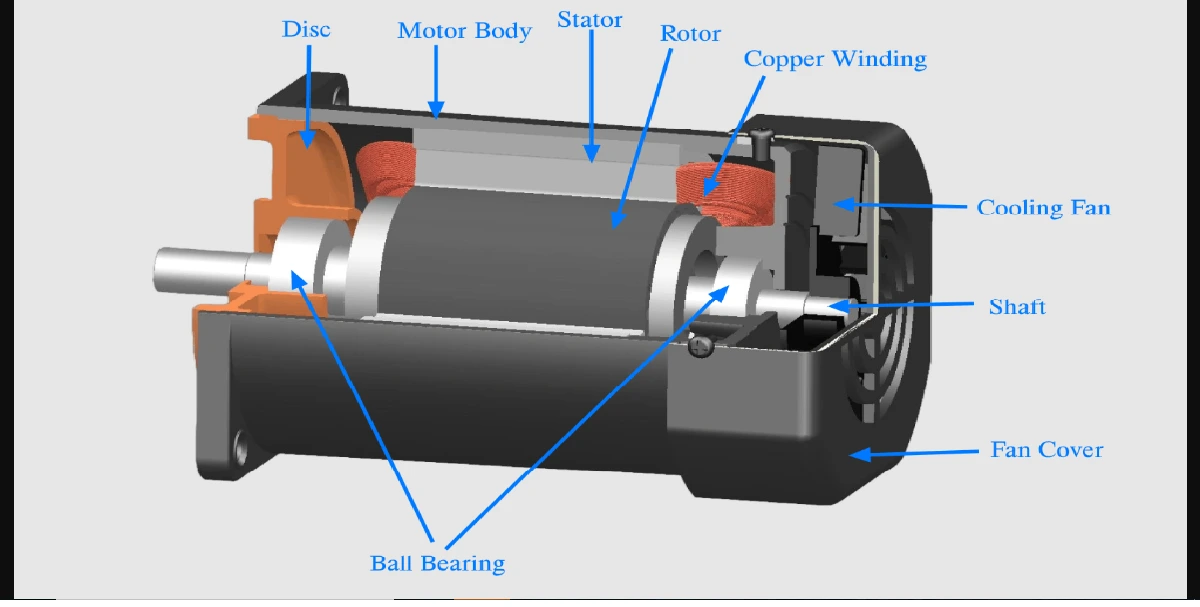
The unit of electric resistance is the ohm(Ω), where one ohm is one volt per ampere. It is defined as the resistance between two points in a conductor when a constant electric potential of one volt applied at the two points produces a current flow of one ampere in the conductor.

Thus, $\begin{aligned} \text { resistance, in ohms R} & =\frac{\text {V }}{\text { I }}\end{aligned}$

where V is the potential difference across the two points, in volts, and I is the current flowing between the two points, in amperes.

The reciprocal of resistance is called conductance and is measured in siemens (S).

Thus, $\begin{aligned} \text { conductance, in siemens G} & =\frac{\text {1 }}{\text { R }}\end{aligned}$

where R is the resistance in ohms.

Find the conductance of a conductor of resistance: (a) 10 Ω (b) 5 kΩ (c) 100 mΩ.

(a) Conductance $G=\frac{1}{R}=\frac{1}{10} siemen =\mathbf{0 . 1} \mathrm{S}$

(b) $G=\frac{1}{R}=\frac{1}{5 \times 10^3} \mathrm{~S}=0.2 \times 10^{-3} \mathrm{~S}=\mathbf{0 . 2} \mathrm{mS}$

Read More Topics

Electrochemical energy storage

Points of consideration for etching process

Primary standard of luminous intensity

Power and signal transmission

Resistance and Conductance – Pedagogy Zone

Santhakumar Raja

Related Categories

Law

Health science